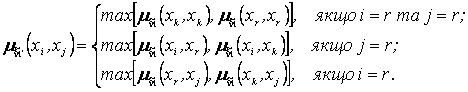Математика. 5.

Скрильник І. І.

Полтавський національний технічний університет імені Юрія Кондратюка

ПОФАРБУВАННЯ ПЛОСКИХ ГРАФІВ ІЗ ВИКОРИСТАННЯМ ОПЕРАЦІЙ НАД НЕЧІТКИМИ ВІДНОШЕННЯМИ

Різноманітні задачі, що виникають при плануванні виробництва, складанні графіків технічного огляду, збереження та транспонування товарів можуть бути представлені часто як задачі теорії графів, тісно пов¢язані з так званою “задачею пофарбування”. Значний інтерес до проблеми пофарбування графів пояснюється можливістю його застосування для вирішення різноманітних оптимізаційних задач. Наприклад, розподілу n ресурсів по n напрямам.

Досліджувалася задача пофарбування плоских графів, яка розгладалася із використанням операцій над нечіткими відношеннями.

Нехай — граф утворений множиною вершин і ребер . Граф вважається правильно пофарбованим у найменшу кількість кольорів, якщо виконуються обмеження:

(1)

де — найменша кількість кольорів. Нехай існує також дві множини і , утворені елементами , такі, що

.

(2)

Тоді є нечітким графом.

Якщо припустити, що , то множина є графом Бержа, таким, що .

Подібно до того, як це робиться в теорії множин, поняття нечіткого графа можна пояснити в термінах поняття носія нечіткого відношення .

Для того, щоб задати нечіткий граф потрібно задати нечітке відношення . Якщо — бінарне відношення на множині , то назвемо матрицею суміжності. Таким чином, зв¢язок із нечітким графом та графом можна виразити через нечітке відношення та матрицю суміжності наступним чином:

(3)

де — відносна відстань Хемінга.

.

(4)

“Слабким ребром” нечіткого графа є значення відношення . “Сильним ребром” нечіткого графа — значення відношення .

Редукцією нечіткого відношення по “слабкому ребру” є операція відшукання індукованого відношення , де , при . Індекси k, r співвідносяться індексу елемента . Отже, індукованого відношення дорівнює:

(5)

Найменшим редукованим відношенням будемо вважати таке відношення, для якого .

Пофарбування нечіткого графа визначається як нечітке відношення .

Задачею знаходження пофарбування нечіткого графа є відшукання такого відображення , при якому .

Якщо перейти від нечіткого пофарбування до чіткого, використовуючи (3), то отримане відношення буде бінарною матрицею пофарбування графа G, котра задовольняє накладеним обмеженням (1).

За результатами дослідження було розроблено програму, яка може бути використана при моделюванні задачі розподілу n ресурсів по n напрямам, а також використовуватися у навчальному процесі.

ЛІТЕРАТУРА

1. Дистель Р. Теория графов. – Новосибирск: ИИМ, 2002. – 335 с.

2. Кристофидес Н. Теория графов. Алгоритмический подход. – М: Мир, 1978. – 427 с.

3. Берж К. Теория графов и её применения. – М: ИЛ, 1962. – 319 с.

4. Белов В.В., Воробьев Е.М., Шаталов В.Е. Теория графов. Учеб. пособие для втузов. – М: Высш. школа, 1976. – 391 с.

5. Скрильник І.І. Застосування генетичного алгоритму для пофарбування n-дольних графів // Материалы II международной научно-практической конференции «Стратегические вопросы мировой науки – 2007». Том 8. Математика, 15 – 28 февраля 2007. – Днепропетровск: Наука и образование, 2007. – С. 17 – 20.

6. Кофман А. Введение в теорию нечетких множеств: Пер. с французского / Под ред. С.И. Травкина. – М: Радио и связь, 1982. – 431 с.

7. Rosenfield A. Fuzzy graphs. – In : Fuzzy Sets and their Applications to Cognitive and Decision Processes. Academic Press, 1975. – P. 77 – 95.

8. Santos E.S. Fuzzy Algorithms // Inform. and Control. Vol. 17, 1970. – P. 326 – 339.

9. Santos E.S. On Reduction of Maximum Machines // Jour. Math. Anal. and Appl, Vol. 37 №3, 1972.

10. Lee E.T., Chang C.L. Some properties of fuzzy logic // Inform. and Control, Vol. 19 №5, 1971. – P. 417 – 431.
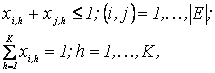
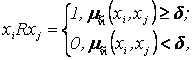
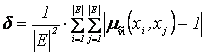