Экономические науки/8. Математические
методы в экономике
к.п.н., доц. Клочко О.В.
Вінницький національний аграрний університет, Україна
Оптимізація
управління запасами
Полегшити завдання пошуку оптимального значення
задачі управління запасами можна за допомогою методів квадратичної апроксимації,
зокрема методу парабол, методу Пауелла. У найпростішому випадку замінюємо
нелінійну функцію f(x) квадратичною функцією q=b0+b1x+b2x2.
Якщо цільова функція f(x) у точках x1, x2, x3
приймає відповідні значення f1, f2, f3, то
можна обчислити коефіцієнти bо, b1, b2 так, що
значення квадратичної функції q(x) = bo + b1(x - x1) + b2(x
- x1)(x - x2) співпадуть зі значенням f(x) у трьох вказаних точках. Нехай функція f(x) визначена на
відрізку [а; b], t і h – додатні постійні числа. Трійку точок х0-t, х0,
х0+h,
що належать [а; b], назвемо опуклою трійкою для f(x), якщо D-(х0)=f(х0-t)-f(x0)³0, D+(х0)=f(х0+h)-f(x0)³0, D++D->0. Якщо трійка точок х0-t, х0,
х0+h
опукла для f(x) то через точки (х0-t, f(х0-t)), (х0,
f(х0)), (х0+h,f(х0+h)) на площині (х, f) можна провести параболу q2(x)=b0+b1x+b2x2
зi старшим
коефіцієнтом b2>0. Ця парабола є графіком звичайного
інтерполяційного многочлена другого степеня і має вид:
q2(x)=f(х0)+![]() (х-х0)+
(х-х0)+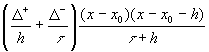
Так як b2=![]() >0, то q2(x) опукла на R1 і досягає своєї нижньої межі на R1 в точці х*=х0+
>0, то q2(x) опукла на R1 і досягає своєї нижньої межі на R1 в точці х*=х0+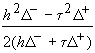
використовуючи умови D-(х0)³0, D+(х0)³0 отримаємо -τ/2<х*-х0<h/2.
Алгоритм методу парабол
Один з варіантів методу парабол для мінімізації
на відрізку [а; b] унімодальної функції f(x). Нехай h>0 - деякий початковий крок, 2h<b-a, х0![]() [а; b]- початкова точка.
[а; b]- початкова точка.
Крок 1. Обчислити f(x0), xi+1=x0+h, обчислити f(x0+h). k=0.
Крок 2.Якщо f(xi+h)≤f(xi).
Перейти до кроку 3. Якщо f(xi+h)≥f(xi).
Змінюємо напрямок пошуку: перепозначимо x0=x0+h. Перейти до кроку 4.
Крок 3. хi+1=хі+h*2і. Перейти до кроку 5.
Крок 4. k=l. хi+1=хі-h*2і.
Крок 5. Перевіряємо, чи хі+1![]() [а; b]:
[а; b]:
Ø Якщо хі+1![]() [а; b], Обчислюємо f(хi+1). Перейти до кроку
6.
[а; b], Обчислюємо f(хi+1). Перейти до кроку
6.
Ø Якщо хі+1![]() [а; b], перейти до кроку 7.
[а; b], перейти до кроку 7.
Крок 6. Перевіряємо, чи утворюють точки хi+1, хi, хi-1 опуклу лінійну комбінацію: Якщо D-(хі)=f(хi-1)-f(xі)³0, D+(хі)=f(хі+1)-f(xі)³0, D++D->0. Перейти до кроку 8. Інакше, при к=0 перейти до кроку 3, при к=1 перейти до кроку 4.
Крок 7. Приймаємо за f(x*)=min{f(u), f(x0), f(x1), ... , f(xn)}, x*=x(fmin),
де u дорівнює а або b в залежності від того який з кінців відрізку ближчий до xі+1.
Кінець алгоритму.
Крок 8. х*=хi-1+![]() . Обчислюємо f(x*), Кінець алгоритму.
. Обчислюємо f(x*), Кінець алгоритму.
У разі необхідності, для уточнення точки мінімуму, можна взяти знайдену точку х* за початкову і повторити процедуру пошуку з початковим кроком h/2. Послідовно повторюючи цей процес, можна знайти точку, що віддалена від множини х* точок мінімуму унімодальної функціїf(x) на відстань, що не перевищує наперед заданого числа. Обчислення наступної точки можна робити за іншим алгоритмом, наприклад xі=xі+h*(i-1) (xі=xі-h*(i-1)).
Розглянемо модель Уілсона, яка є однією з
найбільш розповсюджених моделей управління запасами. Управління запасами є
складовою процесу оптимізації виробничих витрат будь-якої логістичної системи.
В процесі виробництва деякої кількості товару його ціна встановлюється рівною
Р=50 (грн.). Товар зберігається на складі до тих пір, поки не буде
використаний, і вартість зберігання однієї одиниці товару складає Z=4 (грн./кг) в
одиницю часу. Норма споживання товару складає S = 1 (кг) в одиницю часу.
Якщо товар виробляється регулярно в кількості х (кг) на протязі часу x/S, то вартість
функціонування такої системи в одиницю часу f(x)=P*S/x+Z*x/2.
Підставивши дані отримаємо рівняння f(x)=50/x+2*x. В якій кількості необхідно виробляти товар, щоб
вартість функціонування такої системи була мінімальною. (Вартість досягає
мінімуму в точці x=![]() =
=![]() =5 (кг), яка розрахована за умовою оптимальності f(x)/dx=0).
Розв’язати задачу методом парабол.
=5 (кг), яка розрахована за умовою оптимальності f(x)/dx=0).
Розв’язати задачу методом парабол.
Мінімізація на відрізку [1; 10]
унімодальної функції f(x)=50/x+2*x. Нехай h=l, 2h<b-a, тобто 2<10. x0=2![]() [1; 10] - початкова точка.
[1; 10] - початкова точка.
|
№ ітерації |
xi |
f(xi) |
Δ-=f(xi-2)-f(xi-1) |
Δ+=f(xi)-f(xi-1) |
Δ-+ Δ+ |
x* |
f(x*) |
|
1 |
2,0000 |
29,0000 |
|
|
|
|
|
|
2 |
3,0000 |
22,6667 |
|
|
|
|
|
|
3 |
4,0000 |
20,5000 |
6,3333 |
-2.1667 |
|
|
|
|
4 |
6,0000 |
20,3333 |
2,1667 |
-0,1667 |
|
|
|
|
5 |
10,0000 |
25,0000 |
0,1667 |
4,6667 |
4,8333 |
5,5345 |
20,1032 |
|
6 |
6,0345 |
20,3547 |
-4,6667 |
-4.6453 |
|
|
|
|
7 |
5,0345 |
20,0005 |
4,6457 |
-0,3542 |
|
|
|
|
8 |
4,0345 |
20,4621 |
0,3546 |
0,4617 |
0.8159 |
4,9686 |
20,0004 |
Приклад розв'язування задачі з обчисленням наступної точки за алгоритмом xi=x0+h*2(i-l) (xi=x0-h*2(i-l)):
|
№ ітерації |
xi |
f(xi) |
Δ-=f(xi-2)-f(xi-1) |
Δ+=f(xi)-f(xi-1) |
Δ-+ Δ+ |
x* |
f(x*) |
|
0 |
2,0000 |
29,0000 |
|
|
|
|
|
|
1 |
3,0000 |
22,6667 |
|
|
|
|
|
|
2 |
4,0000 |
20,5000 |
6,3333 |
-2,1667 |
|
|
|
|
3 |
5,0000 |
20,0000 |
2,1667 |
-0,5000 |
|
|
|
|
4 |
6,0000 |
20,3333 |
0,5000 |
0,3333 |
0,8333 |
5,1000 |
20,0039 |
Отже, вартість функціонування такої системи мінімальна і дорівнює 20 (грн.), якщо товар виробляється в кількості
х*=4,97 кг. Таким чином, використання чисельних методів оптимізації до
розв’язування економічних задач дозволяє отримати оптимальне рішення та
забезпечує процес прийняття управлінських рішень.
Література:
1. Банди Б. Методы
оптимизации. Вводный курс. - М.: Радио и связь, 1988.
2. Жалдак М.І.,
Триус Ю.В. Основи теорії і методів оптимізації: Навчальний посібник. – Черкаси:
Брама-Україна, 2005. -608 с.
3. Кальченко А. Г.
Логістика: Навчальний посібник. – К.: КНЕУ, 2000.