К. ф-м. н. Редькина Т.В.

Ставропольский государственный университет, Россия

Нелинейное уравнение, связанное с оператором Дирака

Для построения нелинейного уравнения в частных производных используется операторное уравнение нулевой кривизны, где оператор Дирака, взят в качестве оператора рассеяния. К полученному уравнению применены некоторые способы нахождения точных решений присущие уравнениям с солитонными решениями.

Лемма 1. Нелинейное уравнение в частных производных

(1)

имеет операторную структуру нулевой кривизны , и обладает парой Лакса с операторами и А вида:

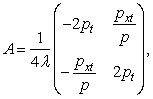
где - произвольный параметр, , - непрерывные функции, зависящие от х, t и дифференцируемые по своим переменным в некоторой области.

Теорема 1. Нелинейное уравнение в частных производных (1) имеет решение, записанное в неявном виде: 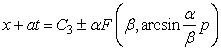, где - произвольные постоянные, - эллиптический интеграл первого рода.

Следствие. Частные решения уравнения (1) имеют вид:

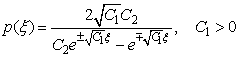, и .

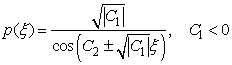Теорема 2. Уравнение (1) имеет автомодельное решение 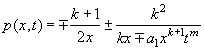, - произвольные постоянные.

Лемма 2. Нелинейное уравнение в частных производных (1) с помощью замены приводится к однородному виду:

(2)

где , - некоторые функции, непрерывные и дифференцируемые по своим переменным в некоторой области, D - оператор дифференцирования, определенный на упорядоченной паре функций следующим образом:

.

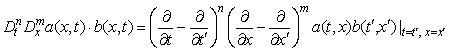Теорема 3. Однородное уравнение (2) имеет решение , где - произвольные постоянные.

Следствие. Уравнение (1) имеет решение вида: 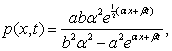где - произвольные постоянные.

Нелинейные уравнения в частных производных могут иметь решения, как с подвижными, так и неподвижными особыми точками. Как показала практика, у решений дифференциальных уравнений обладающих парой Лакса отсутствуют подвижные критические точки. Это означает, что от произвольных постоянных интегрирования может зависеть только положение полюсов.

Теорема 4. Уравнение (1) имеет решение в виде ряда с полюсными особенностями первого порядка 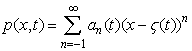, где , , - произвольные функции; , , , остальные коэффициенты определяются рекуррентной формулой

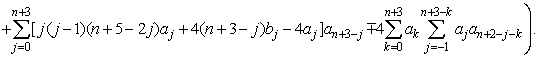
В силу следствий из теоремы Лакса [3] все собственные значения l самосопряженного оператора L являются интегралами движения. Рассмотрим возможность построения законов сохранения, используя уравнение на собственные значения с самосопряженным оператором Дирака первого рода [1]

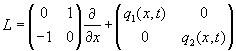, (3)

где - некоторые непрерывные функции, заданные на компактном носителе , - вектор функция.

Теорема 5 Нелинейные уравнения, обладающие парой Лакса с оператором рассеяния Дирака (3), имеют счетное число интегралов движения вида:

где - мнимая единица, определяются по формулам

а остальные функции по рекуррентной формуле

Следствие. Уравнение (1) обладает счетным числом законов сохранения

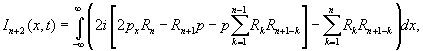
где многочлены определяются по формулам: .

Литература:

1. Б.М.Левитан, И.С.Саргсян, Операторы Штурма-Лиувилля и Дирака. М.: Наука. Гл. ред. физ.-мат. Лит., 1988.

2. А.Д.Полянин, В.Ф.Зайцев, А.И.Журов, Методы решения нелинейных уравнений математической физики и механики. М.: Физматлит, 2005.

3. П.Д.Лакс, Интегралы нелинейных эволюционных уравнений и уединенные волны. – Математика, 13:5, М.: Мир, 1969.