Шилинец В.А., Борис Т.И., Подполухо Е.В.
Белорусский государственный педагогический университет
ОБ ИНТЕГРАЛЬНОМ ПРЕДСТАВЛЕНИИ БИКВАТЕРНИОННЫХ F-МОНОГЕННЫХ ФУНКЦИЙ
В работе [1] предлагается
подход, позволяющий задачи классической механики описать в терминах функций со
значениями в гиперкомплексных числах. Оказывается, можно построить
бикватернионную модель движения тела вблизи поверхности земли и сформулировать
задачу Кеплера на языке дифференциальных уравнений для функций со значениями в
кватернионах. Кроме того, задача о движении твердого тела может быть описана в
терминах функций со значениями в бикватернионах. Так винтовое перемещение
твердого тела можно представить как решение дифференциального уравнения ![]() , где
, где ![]() – бикватернион,
– бикватернион, ![]() – дуальная
переменная,
– дуальная
переменная, ![]() – функция дуальной
переменной со значениями в бикватернионах.
– функция дуальной
переменной со значениями в бикватернионах.
Как известно
[1], бикватернионами (обобщением кватернионов)
называют элементы множества ![]() , где
, где ![]()
![]() ,
, ![]() ,
, ![]() – дуальные числа.
Правило умножения бикватернионов задается правилом умножения мнимых единиц:
– дуальные числа.
Правило умножения бикватернионов задается правилом умножения мнимых единиц: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
В данной
работе для F-моногенных бикватернионных функций, заданных в некоторой
односвязной области ![]() , строится обобщенная интегральная формула Коши.
, строится обобщенная интегральная формула Коши.
Нам
понадобятся следующие определения.
Определение
1. Бикватернионной функцией, заданной в области ![]() , будем называть функцию вида
, будем называть функцию вида ![]() , где
, где ![]() (
(![]() – индекс,
– индекс, ![]() ) – дуальные функции, заданные в области
) – дуальные функции, заданные в области ![]() ;
; ![]() – известный базис
кватернионной алгебры.
– известный базис
кватернионной алгебры.
Далее
полагаем, что ![]() , т.е.
, т.е. ![]() .
.
Определение
2. Бикватернионная функция ![]() называется моногенной
в смысле В.С. Федорова (F-моногенной) [2] по
бикватернионной функции
называется моногенной
в смысле В.С. Федорова (F-моногенной) [2] по
бикватернионной функции ![]() (
(![]() ,
, ![]() (
(![]() ) – действительные числа,
) – действительные числа, ![]() ,
, ![]() ) в области
) в области ![]() , если в этой области найдется такая бикватернионная функция
, если в этой области найдется такая бикватернионная функция ![]() , что
, что
![]() ,
, ![]() ,
, ![]() ,
, ![]() (1)
(1)
(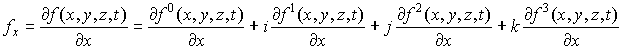
и т.д.).
Обозначим
функцию ![]() через
через ![]() . Тогда равенства (1) можно записать в виде
. Тогда равенства (1) можно записать в виде 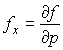 ,
, 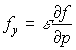 ,
, 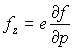 ,
, 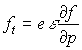 .
.
Пусть ![]() – четырехмерная ограниченная
область с границей
– четырехмерная ограниченная
область с границей ![]() (
(![]() ,
,![]() ). Полагаем далее, что
). Полагаем далее, что ![]() и функция
и функция ![]() ,
,
F-моногенная по ![]() , определены на замкнутой трехмерной поверхности
, определены на замкнутой трехмерной поверхности ![]() , гомеоморфной сфере конечного диаметра и достаточно гладкой
для возможности использовать формулу Остроградского. Для бикватернионной
функции
, гомеоморфной сфере конечного диаметра и достаточно гладкой
для возможности использовать формулу Остроградского. Для бикватернионной
функции ![]() и произвольной точки
и произвольной точки ![]() полагаем [3]:
полагаем [3]:
![]() ,
,
где ![]() – направляющие косинусы внешней нормали к поверхности
– направляющие косинусы внешней нормали к поверхности ![]() в её текущей точке
в её текущей точке ![]()
![]() ,
,
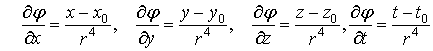 .
.
Пусть ![]() – произвольная данная точка области
– произвольная данная точка области ![]() ,
, ![]() .
.
Теорема
1. Для любой бикватернионной функции ![]() , F-моногенной
по бикватернионной функции
, F-моногенной
по бикватернионной функции ![]() в области
в области ![]() , имеем
, имеем ![]() .
.
Теорема 2. Если бикватернионная функция ![]() является F-моногенной
по бикватернионной функции
является F-моногенной
по бикватернионной функции ![]() в области
в области ![]() , то для любой точки
, то для любой точки ![]() , лежащей внутри
, лежащей внутри ![]() , имеем
, имеем
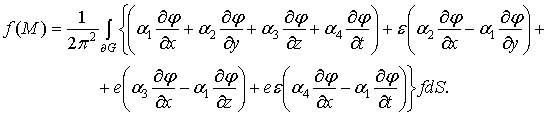 (2)
(2)
Обобщенная
интегральная формула Коши (2) позволяет решить следующую краевую задачу.
Задача. Пусть ![]() – четырехмерная ограниченная
область с границей
– четырехмерная ограниченная
область с границей ![]() (
(![]() ,
,![]() ). Полагаем далее, что бикватернионная функция
). Полагаем далее, что бикватернионная функция ![]() и бикватернионная
функция
и бикватернионная
функция ![]() , F-моногенная по
, F-моногенная по ![]() , определены на замкнутой трехмерной поверхности
, определены на замкнутой трехмерной поверхности ![]() , гомеоморфной сфере конечного диаметра и достаточно гладкой
для возможности использовать формулу Остроградского. Требуется найти в любой
внутренней точке области
, гомеоморфной сфере конечного диаметра и достаточно гладкой
для возможности использовать формулу Остроградского. Требуется найти в любой
внутренней точке области ![]() значение функции
значение функции ![]() , F-моногенной по
, F-моногенной по ![]() , если известны её значения на поверхности
, если известны её значения на поверхности ![]() .
.
Литература
1.
Радыно Н.Я.
О модели описания винтового перемещения твердого тела в терминах бикватернионов
// Международная математическая конференция «Пятые Богдановские чтения по
обыкновенным дифференциальным уравнениям»: тезисы докладов.– Мн.: Институт
математики НАН Беларуси, 2010. – С. 135.
2.
Фёдоров В.С. Основные
свойства обобщённых моногенных функций // Известия вузов. Математика, 1958. –№6. – С.
257–265.
3.
Фёдоров В.С. Об одном
обобщении интеграла типа Коши в многомерном пространстве // Известия вузов.
Математика, 1957. –№1. –С.227–233.