К. ф.-м. н. Бородачева Е. В.

Самарский государственный университет, Россия

Об аппроксимации сверху дифференциальных включений

при наличии быстрых переменных

Пусть −n-мерное евклидово пространство со скалярным произведением < ∙ , ∙ > и соответствующей нормой ||∙||, − совокупность всех непустых компактов из , − совокупность всех непустых выпуклых компактов из , − расстояние от точки до множества , − полуотклонение по Хаусдорфу множества от множества , − расстояние по Хаусдорфу между компактами и , , − модуль множества . Пусть далее, – совокупность локально интегрируемых (по Лебегу) функций , для которых найдутся константы и такие, что при для каждого выполняется неравенство:

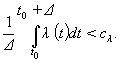(1)

Кроме того, пусть – совокупность всех функций

, непрерывных в 0, для которых .

В работе рассмотрена задача Коши для системы дифференциальных включений с медленными () и быстрыми () переменными:

(2)

в которой отображения – малый параметр.

Как известно [1], при аппроксимации сверху задачи (2) ей ставится в соответствие так называемая усредненная задача Коши:

(3)

с отображением При этом задача (3) достаточно адекватно отражает основные свойства медленных переменных системы (2). Напомним определение аппроксимации сверху задачи (2) задачей (3).

Определение. Задача (3) называется аппроксимирующей сверху задачу (2), если для любого существует такое, что для любого и для любого решения задачи (2) найдется решение задачи (3), для которого выполняется условие:

(4)

Вопрос об аппроксимации сверху задачи (2) хорошо изучен в случае, когда отображения из правых частей дифференциальных включений задачи (2), а также отображение являются липшицевыми по и по соответственно отображениями. В этом случае при некоторых условиях, естественных для задач аппроксимации, доказано [2], [3], что задача (3) аппроксимирует сверху задачу (2). При отсутствии в задаче (2) быстрых переменных результаты по аппроксимации сверху задачей (3), также в предположении липшицевости отображений из правых частей исходной и усредненной задач, подробно изложены в [4]. Отмечу однако, что стандартная процедура усреднения, позволяющая в ряде случаев найти вид усредненной задачи (3), в случае нелипшицевых по отображений и может привести к усредненной задаче (3) с нелипшицевой правой частью . Данная работа посвящена рассмотрению такого случая. Доказана теорема о том, что при выполнении для отображений и некоторых условий, как обычных для задач аппроксимации, так и новых (более слабых, чем липшицевость) задача (3) аппроксимирует сверху задачу (2). Заметим, однако, что возможность аппроксимации сверху в не липшицевом случае доказана в [5], но при других условиях и в случае, когда задача (2) – это задача Коши для сингулярно возмущенных дифференциальных включений с медленными и быстрыми переменными.

Пусть далее для и выполнены следующие условия:

1) и измеримы по на для любых и для любого .

2) Отображения и интегрально ограничены функциями и

, то есть

3) Условие близости средних от и :

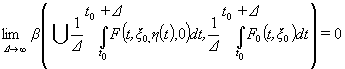(5)

равномерно по начальным условиям задачи

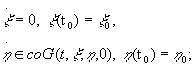(6)

объединение в (5) берется по всем решениям этой задачи (6).

4) Для любых (– некоторое число), и таких, что имеют место оценки:

здесь

5) Найдутся функции такие, что для любых выполняются неравенства:

Следуя [6], будем называть многозначное отображение односторонне липшицевым (OSL) по , если найдется локально интегрируемая (по Лебегу) в функция такая, что существует вектор для которого .

Отметим, что для однозначных функций это условие появилось впервые, по-видимому, в [7] в связи с вопросом о единственности решения задачи Коши для системы обыкновенных дифференциальных уравнений.

Условие OSL является обобщением хорошо известного условия липшицевости. А именно, если отображение липшицево по при каждом с функцией то оно тем более будет и OSL, причем с той же функцией . Обратное же, вообще говоря, не верно.

Основным результатом данной работы является следующая теорема.

Теорема. Пусть задача (2) имеет хотя бы одно решение на при каждом и выполнены условия 1)‒5). Предположим, кроме того, что отображение при каждом удовлетворяет условию OSL по с константой , а отображение является OSL по с функцией такой, что при

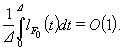
Тогда задача (3) аппроксимирует сверху задачу (2).

Следующий пример иллюстрирует сформулированную теорему.

Пример. В качестве исходной задачи рассмотрим такую задачу Коши для системы дифференциальных включений с медленными и быстрыми переменными:

(7)

с отображениями , задаваемыми соответственно равенствами:

в которых функция определяется так:

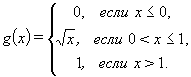
Усредненная задача (3) в данном примере имеет вид:

(8)

в которой отображение определяется таким равенством:

Очевидно, что отображения и не являются липшицевыми по и по соответственно. Поэтому известные теоремы об аппроксимации сверху в липшицевом случае для задач (7) и (8) не применимы при решении вопроса об аппроксимации сверху задачи (7) задачей (8). Можно показать, что для задач (7) и (8) выполнены все условия сформулированной выше теоремы об аппроксимации сверху в случае OSL отображений. Согласно этой теореме усредненная задача (8) аппроксимирует сверху исходную задачу (7).

Литература:

1. Филатов О. П., Хапаев М. М. Усреднение систем дифференциальных включений. М.: Изд-во МГУ, 1998.

2. Филатов О. П., Хапаев М. М. Усреднение дифференциальных включений с «быстрыми» и «медленными» переменными // Матем. Заметки. 1990. Т. 47. № 6. С. 102-109.

3. Филатов О. П., Хапаев М. М. О взаимной – аппроксимации решений системы дифференциальных включений и усредненного включения // Матем. Заметки. 1990. Т. 47. № 5. С. 127-134.

4. Плотников В. А., Плотников А. В., Витюк А. Н. Дифференциальные уравнения с многозначной правой частью. Асимптотические методы. Одесса: Астропринт, 1999.

5. Donchev T., Slavov I. Averaging method for one-sided Lipschitz differential inclusions with generalized solutions // SIAM J. Control Optimization. 1999. V. 37. № 5. P. 1600-1613.

6. Donchev T., Farkhi E. Stability and Euler approximation of one-sided Lipschitz differential inclusions // SIAM J. Control Optimization. 1998. V. 36. № 2. P. 780-796.

7. Красносельский М. А., Крейн С. Г. Нелокальные теоремы существования и теоремы единственности для систем обыкновенных дифференциальных уравнений // Докл. АН СССР. 1955. Т. 102.№ 1. С. 13-16.

8. Благодатских В. И., Филиппов А. Ф. Дифференциальные включения и оптимальное управление // Тр. МИАН. 1985. Т. 169. С. 194-252.