Chernova E.S.

Kemerovo State University, Russia

Conditions For Optimality of Trajectories In One Model For Sustainable Development of Economic Region

I. Introduction

The term “sustainable development” can be defined as “development that meets the needs of the present without compromising the ability of future generations to meet their own need” [1]. The field of sustainable development can be conceptually broken into three constituent parts: environmental sustainability, economic sustainability and social sustainability. 

Today sustainable development problems of human society, single countries and regions attract attention of specialists in different areas of knowledge (e.g. [3, 4, 8, 9]). At the same time, it should be observed that there is no general methodology of the research of this new extensive field of human activity. One of the analysis techniques in searching for the solution of this global problem can become mathematical modelling. At present time there are some attempts of building appropriate mathematical models for sustainable development based on so-called global models already existent.    

II. Model Assumptions and Requirements

For formalization of the regional sustainable development problem we modified the global model “World 3” [10] because of the following reasons. In this model economic and environmental parts are represented in a relatively complete form in contrast to, for example, “Strategy for Survival Project” of Mesarovic and Pestel or the Latin American World Model [7], where environmental problems were not covered at all. On the other hand, disaggregation level in “World3” is higher than in the model “World2” [6], which can give an opportunity to use it at regional level, whereas the use of the model “World2” can be incorrect in this case (see also [5]). 

Mathematical modelling for sustainable development of region was carried out on the assumption that in terms of sound economy there exists such an initial condition, from which it is possible to turn to sustainable development.

Besides, for further building and research of the model, the following assumptions should be made.

·        The industrial output I (t) in a year t, population in the 2nd (15 – 44)  and in the 4th (after 65)  age groups, as well as the total fertility rate  and the value of desired fertility  will be considered to be determined from statistics by prediction.

·        The cost of developing 1 hectare of land , the agricultural investment rate in land development , land degradation rate , land regeneration time , pollution generation rate , pollution absorption time , death rate in different age groups , i = 1,…,4, will be assumed to be constant. All of them were represented by tabular functions in the model “World3” (except for , which had tabular functions as an argument). These values were obtained by statistics processing over developed countries and based on historical trends and arrangements existed at that moment. It will be illegal to use these functional dependencies from “World3” in the model for sustainable development of region.    

·        Land erosion rate will be considered to be in direct proportion to the amount of the already existent erosive lands with proportionality constant . In much the same way, nonrenewable resources decrease with the constant rate  and urbanization rate is equal to .

·        Let us also introduce a prosperity index , that will be directly proportional to the service capital stock  and inversely proportional to the population size p.

After analyzing sustainable development problem description, there were marked out the following fundamental requirements to the mathematical model for sustainable development [3]: the presence of social, economic and environmental sectors in the model; controllability of the model; the presence of a vector cost functional in the model. 

III. Modelling

We shall transform the model “World3” according to the listed above requirements and assumptions. Capital investment allocation is the easiest and most natural mechanism for development control of socio-economic system. Therefore, we shall take investment rates in different spheres from “World3” as control variables, whereas, in the model “World3”, they were determined either as the tabular functions (that excluded beforehand the opportunity of any deliberate human interference in the system functioning) or were not taken into consideration at all. They are the rates of the industrial output distributed to industry, service, food production, eroded soil restoration, restoration of nonrenewable resources, pollution elimination and birth control.

As for the presence of three submodels, capital and agriculture systems of the model “World3” are referred to the economic submodel; nonrenewable resources and pollution systems are referred to the environmental submodel, and population system is referred to the social submodel of the mathematical model for sustainable development. 

Let  and  denote, respectively, the investment rates in industry and service. Then equations of the industrial and service capital stocks will be:

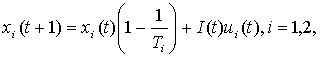                              (1)

where , i=1,2, denotes, respectively, industrial and service capital lifetimes.

Consider agriculture system. Let  denote investment rate in food production and let’s introduce  as investment rate in eroded soil restoration. Then equations for the amount of potentially arable land and of eroded soil will be:

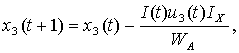                                       (2)

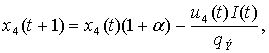                                    (3)

where  = const denotes recovery value of 1 hectare of land.

Let’s introduce additional terms in the equations of value of nonrenewable resources and of pollution level. They will be assigned to restoration of resources and pollution elimination. So the equations, respectively, take the following form:

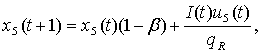                                    (4)

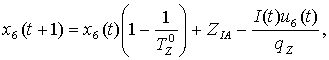                             (5)

where  is investment rate in resource restoration,  is investment rate in pollution control,  = const is recovery value of one unit of pollution, = const is recovery value of one unit decontamination.

Finally, we add one control variable  to the population system. It will denote investment rate in birth control. Then the equation of population in the 1st age group will take the form:

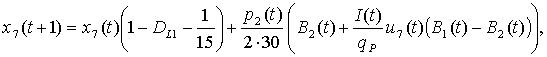      (6)

where  const denotes the highest possible budget of money for birth control.

Auxiliary equations of the model will include the equation of inherent land fertility, the equation of amount of urban land used, the equation of the amount of cultivated land, the equation of population in the 3rd age group and also the equation of  total population (see [2]). 

Consider the algebraic path constraints of our model. Obviously, it will include the following:

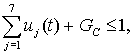                                                                      (7)

where = const denotes investment rate in the production of consumer goods.

Let , j = 1,…,7, designate the minimum rate of the industrial output, assigned to each sphere at each instant of time. Then:

, ,                                                                (8)

The model will also include obvious nonnegativity constraints (for the pollution level, the amount of potentially arable land, the amount of eroded soil and the value of nonrenewable resources) and the condition, according to which the resource restoration will not be able to give more resources than nature. Thus, the model will contain the following algebraic path constraints:

, , , .                (9)

There should be at least three cost functional in the obtained problem [3]. In the environmental sphere it will be logical to minimize the pollution level. The cost functional in the economic sphere will be defined as the production costs to minimize. Finally, in the social sphere it is acceptable to consider the prosperity index (introduced above), which should be maximized as the cumulated measure of the service level. Thus, the model will include the following three cost functionals:

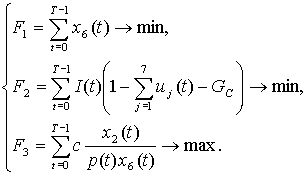                             (10)

There also will be present boundary conditions for all the seven states in the model. Thus, the built model is a discrete-time optimal control problem with many cost functionals, where (1) – (6) are the equations of motion (dynamic constraints), (7) – (9) are the algebraic path constraints, (10) is the vector cost functional.

IV. Trajectory Optimization

In order to prove the necessary condition for an optimal trajectory in (1) – (10) (with boundary conditions) we use Pontryagin's maximum principle.

We use the weighted-sum method for solving the given multi-criteria problem. Let  denote the weighted sum of F1, F2, F3 with the weights , ,  respectively.

Rewrite equations (1) – (6) in the following unified form:

.                       (11)

Since sets , where U is the set of admissible values of the control variables, are convex, the function f 0(x,u) is linear in u, then optimal control u* will maximize the Hamiltonian:

,        (12)

in u(t)ÎU, t = 0,…,T – 1, where  denotes the scalar product of the vectors  and and  is the solution of the costate equations.

H is linear in u (t) = , t = 0,…, T – 1, therefore it will attain a maximum on the edge of the polytope, defined by U(t). Concrete values of uj*(t) can be found by comparing values at the vertices of this polytope, using simplex method.

The vector x(t) will be then defined from (11) by substitution of the obtained u*(t).

                       (13)

Since the considered system (1) – (6) is linear (both in x and u) then discrete-time Pontryagin's maximum principle provides also sufficient conditions for an optimum. Thus, we have proved the following theorem.

Theorem Control u* is optimal in (1) – (10) if and only if it maximizes the Hamiltonian (12), t = 0,…,T – 1, where , j=1,…,7, are evaluated by the following formulas:

,

,

,

, .

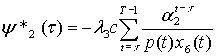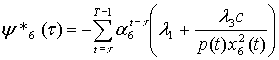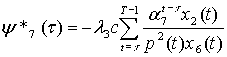Thus, we obtained necessary and sufficient test for optimality of trajectories for the model (1) – (10).

References

1.     Brundtland, G. H. (ed.), Our Common Future: World Commission on Environment and Development. Oxford: Oxforn University Press, 1987.

2.     Chernova, E. S., Vychislenie optimal'noj traektorii v modeli ustojchivogo razvitija regiona, postroennoj v forme modificirovannoj global'noj modeli «Mir-3». In Bulletin of Kemerovo State University, ¹ 2, Kemerovo, 2009, pp.48–51.

3.     Danilov, N. N., Ustoichivoe razvitie: metodologiya matematicheskikh issledovanii. In Bulletin of Kemerovo State University. Matematika, vyp. 4, Kemerovo, 2000, pp. 5–15.

4.     Danilov-Danil’yan, V. I., Losev, K. S., Reyf, I. E., Sustainable Development and the Limitation of Growth: Future Prospects for World Civilization. Berlin: Springer, 2009.

5.     Egorov, V. A., Kallistov, V. N., Mitrofanov, V. B., Piontkovskij, A. A., Matematicheskie modeli global'nogo razvitija. Leningrad: Gidrometeoizdat, 1980.

6.     Forrester, J. W., World Dynamics. Cambridge, Mass: Wright-Allen Press, 1971.

7.     Herrera, A. O., Scolnik, H. D., Chichilnisky, G., Gallopin, G. C., Hardoy, J. E., Mosovich, D., et al., Catastrophe or New Society? A Latin American World Model. Ottawa: International Development Research Centre, 1976.

8.     Hersh, M. Mathematical modelling for sustainable development. Berlin: Springer, 2005, pp. 75-529.

9.     Koptjug, V. A., Na puti k ustojchivomu razvitiju civilizacii. In Svobodnaja mysl', ¹14, Moscow, 1992, pp. 3–16.

10. Meadows, D. H., Behrens III, W. W., Meadows, D. L., Naill, R. F., Randers, J.,  and Zahn, E. K. O., The Dynamics of Growth in a Finite World. Cambridge, Mass: Wright-Allen Press, 1974.