Физика /1. Теоретическая физика

Д. ф.м.н. Ольховский В.С.

Институт ядерных исследований НАНУ, Kиев-0650, Украина

О времени как квантовой наблюдаемой, канонически сопряжённой энергии

1.Введение. Уже долгое время (начиная с работы Паули [1]) известно, что время не может быть представлено самосопряжённым линейным оператором. То, что время не может быть представлено самосопряжённым оператором, следует из полуограниченности непрерывных спектров энергий (обычно они снизу ограничены нулём). Такая ситуация явно не укладывается в рамки обычных ожиданий того, что время, как и пространство, в одних случаях играет роль простого параметра, а в других является физической наблюдаемой, которую следовало бы представить оператором. Список работ, посвящённых проблеме времени в квантовой механике, велик. Однако, в ряде работ была проигнорирована теорема Наймарка из [2], которая явилась основанием авторских результатов. В этой теореме говорится [2], что неортогональное спектральное разложение E(l) эрмитового оператора H принадлежит к типу Карлемана [3] (и оно единственно для максимального эрмитового оператора), т.е. оно может быть аппроксимировано последовательностью самосопряжённых операторов, спектральные разложения которых слабо сходятся к спектральному разложению E (l) оператора H .

Именно с помощью этой теоремы Наймарка было показано в [4-8], что время может быть введено как квантово-механическая наблюдаемая, канонически сопряжённая энергии, для физических систем с непрерывными спектрами энергий. При этом было показано, что оператор времени для таких систем обычно является максимальным эрмитовым оператором. А в [6-8]) было выяснено, что для систем с дискретными спектрами энергий время также является квантово-механической наблюдаемой, канонически сопряжённой энергии, а оператор времени является квази-самосопряжённым оператором.

2. Время как квантовая наблюдаемая и общее определение средних времён квантовых процессов. VM approach!Следуя [5-8], для систем с непрерывными спектрами энергий для времени вводится оператор , канонически сопряжённый энергии:

ì t во временном представлении, (1а)

=í

î–ihв энергетическом(E-) представлении. (1b)

Он является не самосопряжённым, но эрмитовым и действует на квадратично интегрируемые пространственно-временные волновые пакеты в представлении (1a), и на их Фурье-преобразования в представлении (1b) при исключении точки E=0. Это условие достаточно, чтобы оператор (1a,b) был “максимальным эрмитовым оператором” [5-8] (в соответствии с терминологией [9]. И при этом исключение точки E=0 не ограничивает физической общности, поскольку состояния “покоя” с нулевой скоростью не наблюдаемы.

Оператор (1b) определяется как действующий на пространство P непрерывных дифференцируемых квадратично интегрируемых функций f (E), удовлетворяющих условиям

|f (E)|² dE < ∞; |∂f (E) / ∂E|² dE < ∞; |f (E)|² E² dE< ∞ (2)

и

f(0)=0. (3)

Пространство P плотно в Гильбертовом пространстве функций L² , определённых (только) на полу-оси 0 ≤ E < ∞. Вполне очевидно, что оператор (1a,b) эрмитов, т.е. соотношение (f_1, f₂)=((f₁), f₂) имеет место тогда и только тогда, когда все квадратично интегрируемы функции f(E), в пространстве которых он определён, исчезают в точке E=0. Оператор не имеет эрмитовых расширений, ибо иначе можно было бы найти хотя бы одну функцию f₀ (E), удовлетворяющую условию f₀(0)¹0, но это несовместимо со свойством эрмитовости. Поэтому является максимальным эрмитовым оператором.

Именно в силу этих причин Паули ранее отверг использование оператора времени (см., напр., [1]) и это почти на 60 лет практически остановило изучение времени как квантовой наблюдаемой (потому что работа Наймарка [2], равно как и более давняя работа Карлемана 1923г [3], были долго неизвестны физикам в квантовой механике. Но, тем не менее, фон Нейман ещё в [10] утверждал, что использование только самосопряжённых операторов в квантовой механике может быть слишком большим ограничением. Для пояснения такой своей мысли он сам выдвинул такой пример: Рассмотрим частицу, свободно движущуюся в пространстве с полуосью x (0≤ x< ∞), которое ограничено жёсткой стенкой вдоль плоскости x=0. Оператор x-компоненты импульса для такой частицы определён (только) на пространственной полуоси 0<x<∞. Поэтому он имеет те же свойства, что и оператор (1a,b) и, следовательно, является не самосопряжённым оператором, но максимальным эрмитовым оператором. Тем не менее, он продолжает оставаться наблюдаемой с очевидным физическим смыслом. Такими же свойствами обладает и оператор радиального импульса (0<r<¥).

Для завершения изучения времени как наблюдаемой в квантовой механике остаётся решить вопрос о мере (или весовой функции) усреднения по времени в согласовании с процедурами усреднения и известными принципами квантовой механики. В случае одномерного и однонаправленного движения частицы такая мера (или весовая функция) может быть получена с помощью простой величины

W (x,t)dt = 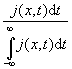, (4)

где вероятностная интерпретация of j(x,t) соответствует плотности потока вероятности прохождения частицей через точку x в момент t (более точно, в течение единичного интервала времени с центром в момент t), при движении частицы в положительном x-направлении. Эта мера не постулируется, а просто является прямым следствием известной вероятностной (пространственной) интерпретации плотности вероятности r(x, t)и уравнения непрерывности

¶r (x,t)/¶t + div j(x,t) = 0 (5)

при движении частицы в поле любого гамильтониана, описываемого одномерным уравнением Шредингера. Вспомним, что здесь r (x, t) есть вероятность нахождения движущейся частицы в единичном пространственном интервале с центром в точке x в момент времени t. Плотность вероятности r(x,t) и плотность потока вероятности j(x,t) связаны с волновой функцией Y (x,t) частицы обычными соотношениями r(x,t)=|Y(x,t)|² и j(x,t) = Re [Y*(x,t) (h/im) ¶Y(x,t)/¶x]. Мера (4) впервые была введена и исследована в [6-8].

Если плотность потока j(x,t) меняет свой знак, то величина W(x,t)dt уже не является положительно определённой величиной и приобретает физическое значение плотности вероятности только в течение тех ограниченных интервалов времени, в которых плотность потока j(x,t) сохраняет свой знак. В этом случае естественно ввести две меры, разделяя положительные и отрицательные значения потоков вероятности по знаку:

W_±(x,t)dt=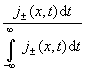 (4a)

с j_±(x,t)=j(x,t)Q(±j), где Q(z) – ступенчатая функция Хэвисайда, равная нулю при z < 0 и единице при z > 0.

Cреднее значение <t(x)> в момент времени t, в который частица проходит через точку x (проходя её в одном только направлении x), и среднее значение <t_± (x)> в момент времени t, в который частица проходит через точку x, проходя её в положительном или отрицательном направлении оси x, можно определить как

<t(x)>=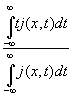=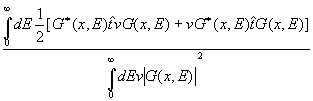, (6a)

где G (x,E) – Фурье-преобразование движущегося одномерного (1D) волнового пакета Y(x,t)=G(x,E)exp(–iEt/h)dE=g(E)j(x,E)exp(–iEt/h)dE при переходе от временного представления к энергетическому, и

<t_± (x)> = 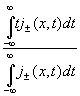, (6b)

соответственно, а также и средние длительности 1D прохождения частицы от точки x_i к точке x_f >x_i и 1D отражения частицы от области (x_{i ,}¥) в область x_f £x_i :

<t_T (x_i ,x_f)> = <t₊ (x_f)> –<t₊(x_i)> и <t_R (x_i ,x_f)> = <t_– (x_f)>–<t₊(x_i)>, (6c)

соответственно.

В [6-8] было показано, что для максимального эрмитова оператора и самосопряжённого оператора энергии выполняется соотношение неопределённостей DE× Dt³ h /2.

Таким образом, для квантово-механических систем с непрерывными спектрами энергий математические свойства максимальных эрмитовых операторов, в том числе и оператора в соотношениях (1), вполне достаточны для того, чтобы полагать их квантовыми наблюдаемыми: Именно, единственность разложения единицы (называемой также спектральной функцией) для операторов и, кстати, ⁿ (n>1) гарантирует эквивалентность средних значений аналитических функций времени, вычисленных как в t-, так и в E-представлениях.

С этой точки зрения, нет никакого практического (физического) различия между самосопряжёнными и максимальными эрмитовыми операторами для систем с непрерывными спектрами энергий. Поэтому подчеркнём, что математических свойств ⁿ (n³1) вполне достаточно для того, чтобы считать время квантово-механической наблюдаемой (подобно энергии, импульсу, пространственным координатам,...) без введения новых физических постулатов.

В случае уравнения Клейна-Гордона [11, стр. 63-65] уравнение непрерывности будет (5), где после перехода в импульсное пространство для частиц r=|Y(x,t)|²= ,a - элемент лоренц-инвариантной меры на гиперболоиде k²=m₀². Тогда мера усреднения по времени одномерно движущейся частицы (или анти- частицы) будет (4) или (4а), как и в нерелятивистском случае.

В случае уравнения Дирака [11, стр.74-75] уравнение непрерывности тоже будет (5),

0 s_k 0 1 0 -i

где r =|Y(x,t)|², j_k = cY ^*(x,t)a _kY (x,t), a _k=(s_k 0 ), s₁ =(1 0), s₁ =(i 0 ).

И тогда мера усреднения по времени одномерно движущейся частицы (или античастицы) будет также (4) или (4а).

Что касается соотношения неопределённостей энергии и времени, то их вывод для релятивистских квантовых уравнений Клейна-Гордона и Дирака практически совпадает с соотношением неопределённостей в нерелятивистской квантовой механики.

Далее, ситуация с дискретным спектром энергий для оператора времени в релятивистской квантовой механике тоже практически совпадает с дискретным спектром энергий для нерелятивистской квантовой механики.

5. Временной анализ квантовых процессов.

(1) В [6-8] также показано, что время можно считать квантовой наблюдаемой, канонично сопряжённой энергии не только в квантовой механике, но и при одномерном движении фотонов в квантовой электродинамике.

(2) Временной анализ процессов туннелирования частиц и фотонов позволил получить следующие результаты:

(a) В [12] было установлено, что практически все известные ранее частные определения и рецепты определений оказались в рамках общего определения Olkhovsky-Recami (O-R) простыми частными случаями или среднего времени туннелирования, или средне-квадратичной флуктуации в распределении времён туннелирования.

(в) Хотя и нет прямого предельного перехода к классической механике для туннелирующих под потенциальным барьером частиц, тем не менее, существуют ненулевые плотность вероятности и плотность потока вероятности движения волновых пакетов внутри таких барьеров и, более того, для движения суперпозиции затухающих и анти-затухающих волн волновых пакетов под барьером существует явно прямой классический предел: вспомним аналогичное движение во времени волновых пакетов, описываемых суперпозициями затухающих и анти-затухающих волн в классической оптике и классической акустике (см., напр., [13,14]).

Литература.

1. Паули В. Общие принципы волновой механики (М.-Л.: ОГИЗ, 1947) (см. стр.102-103).

Pauli W., in: Handbuch der Physik, vol.5/1 ( ed. by S.Fluegge) (Berlin, 1926), (p.60).

2. Наймарк М..А. Изв.АН СССР, сер. матем., 4 277 (1940).

3. Carleman T. Sur les e’quations i’ntegrales a’ noyau re’el et syme’trque (Uppsala,1923).

4. Ольховский В.С. Укр. физ. журнал 18 1910(1973); Olkhovsky V.S. et al, Nuovo Cim. A22

263(1974); Ольховский В.С., ФЭЧАЯ, 15 290(1984).

5. Holevo A.S. Rep. Math. Phys. 13 379(1978); Холево А.С. Вероятностные и

статистические аспекты квантовой теории (М.: Наука, 1980).

6. Olkhovsky V.S., Recami E. I.J.Mod.Phys. A22 5063 (2007); I.J.Mod.Phys. B22 1877 (2008).

7. Olkhovsky V.S. Advances in Mathem.Phys.,2009 (2009),аrticle ID 859710, 83 pages,

doi:10.1155/2009/859710.

8. Ольховский В.С., Успехи физ.наук,181: N8 (2011)859.

9. Ахиезер Н.Н., Глазман И.М., Теория линейных операторов в гильбертовом

пространстве (М.: Наука, 1966).

10. фон Нейман И., Математические основы квантовой механики, М.: Наука, 1964).

11. Швебер C., Введение в релятивистскую квантовую теорию поля ,М.,ИИЛ,1963 (842 с.).

12. Olkhovsky and Recami E. Phys. Reports, 214 339(1992); Olkhovsky V.S. et al Phys.Rep.

398133(2004).

13. Chew H. et al, Applied Optics 18 2679 (1979).

14. Chandiramani K.L., J.Acoustical Soc.Am. 55 19 (1974).