Сериков В.И., Воронин С.В.

Липецкий государственный технический университет, Россия

Принцип соответствия и уравнение непрерывности для модифицированного уравнения Клейна – Гордона.

Связь между нерелятивистским уравнением Шрёдингера и его релятивистским аналогом обычно рассматривается на операторном уровне. Однако в духе принципа соответствия должен существовать более простой предельный переход от релятивистской формы уравнения Шрёдингера к нерелятивистскому уравнению. В настоящей работе нами рассматривается такой предельный переход для модифицированного релятивистского уравнения Шрёдингера. Для этой цели мы рассматриваем уравнение

(1)

где , Это уравнение при переходит в нерелятивистское уравнение Шрёдингера и отличается от уравнения Клейна – Гордона [1] только константой в операторе правой части. Таким образом, модифицированное уравнение Клейна – Гордона (1) удовлетворяет принципу соответствия. Связь этого уравнения с уравнением непрерывности также отличается от той, которая имеет место для уравнения Клейна – Гордона. Представляя уравнение (1) в форме

(2)

а затем, действуя стандартно [2], то есть, рассматривая вместе с уравнением (2) комплексно-сопряжённое ему уравнение и проводя обычные преобразования, получим уравнение вида

(3)

которое представляет собой уравнение непрерывности

(4)

где введены обозначения:

(5)

(6)

Выражение (6) для плотности тока совпадает с аналогичным выражением для плотности тока в нерелятивистской теории, а выражение для плотности содержит слагаемое, которое исчезает при (т.е. в нерелятивистском пределе). Таким образом, выражения (5) и (6) подчиняются принципу соответствия. Поскольку выражение (5) имеет смысл числа частиц n в единице объёма, то необходимо рассмотреть вопрос о неотрицательности этого выражения, что обеспечивается условием

(7)

Для состояний частиц с определённой энергией () имеем , , так что значение выражения (7) равно и положительно. Волновое уравнение (2) допускает отрицательные значения энергии, однако интерпретация таких решений по Фейнману и Штюкельбергу [3] (как состояний с обращённым временем) позволяет рассматривать значения выражений (7), как положительные. Можно предложить ещё одну интерпретацию для отрицательных значений плотности ρ, если принять во внимание, что физический смысл имеет лишь величина . Рассматривая в качестве определения элемента объёма величину , можно ввести отрицательный элемент в форме . Теперь для отрицательных значений величины можно полагать, что отрицательное значение связано с элементом , что обусловлено только перестановкой ортов (и эквивалентно переходу от правой тройки ортов к левой) и не изменяет физического смысла.

Рассматривая преобразование , которое позволяет перейти от уравнения (2) к уравнению Клейна – Гордона для функции , и используя в соотношении (5) имеем

(8)

Таким образом, преобразование оставляет в выражении плотности только релятивистскую часть, следовательно, принцип соответствия выполняется. Уравнение (2) может также быть представлено в виде

(9)

где представляют собой операторы – кватернионы, и – матрицы Паули, , , – компоненты оператора импульса . Следует отметить, что уравнение (2) имеет вид аналогичный нерелятивистскому уравнению Шрёдингера. Оператор в правой части уравнения (2) эрмитов, то же относится и к уравнению (9). Это обстоятельство показывает существенное отличие рассматриваемого представления от имеющегося в литературе [1], так как эрмитовость оператора в правой части должна приводить к положительно-определённой сохраняющейся вероятности.

В электромагнитном поле уравнение (1) имеет вид

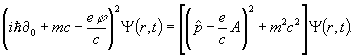(10)

Отметим здесь, что решения уравнения (10) связаны с решениями уравнения Клейна – Гордона в электромагнитном поле преобразованием

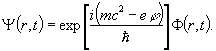(11)

Используя, как и в уравнении (9), для записи правой части кватернионы, уравнение (10) можно представить в форме

(12)

где , – операторные кватернионы обобщённого импульса, 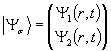, спиновая волновая функция (в уравнении (9) такая запись не использовалась, так как спиновые степени свободы не затрагиваются). Такая форма аналогична представлению уравнений (2) и (12) с помощью смешанных спин-тензоров валентности (1,1) [5]. Записывая уравнение (12) в развёрнутой форме, имеем

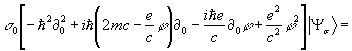
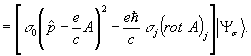(13)

Действуя так же, как и в уравнении (2) , получим уравнение вида

(14)

Здесь учтено, что второй член в правой части уравнения (14) при подстановке спиновых волновых функций обращается в ноль. Таким образом, при наличии электромагнитного поля, имеем

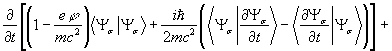
(15)

Уравнение (15) представляет собой уравнение непрерывности, в котором

(16)

(17)

Выражение (17) представляет собой плотность тока вероятности в присутствии магнитного поля, а выражение (16) помимо поправки, связанной с электрическим потенциалом, содержит релятивистскую поправку, рассмотренную выше.

В уравнении (10) можно перейти к «ковариантным производным» [6], то есть операторам вида , , после чего оно принимает форму

(18)

где , . Такая форма позволяет судить об инвариантности уравнения (18) по отношению к калибровочным преобразованиям электромагнитного поля: , .

Используя в формуле (10) тождество

(19)

запишем уравнение (10) в виде

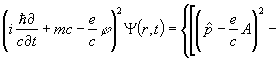
(20)

И здесь, раскрывая скобки в левой части уравнения (20), опуская члены, содержащие в знаменателе c² и, вводя напряженность магнитного поля , приходим к уравнению Паули.

Отметим, что использование тождества (19) приводит к существенным результатам только при наличии векторного потенциала , который представляет собой аксиальное векторное поле. Таким образом, аксиальное векторное поле, дающее вклад в импульс частицы проявляет скрытые (спиновые) степени свободы. Уравнение (10) в форме (20) имеет в качестве решений волновые функции, обладающие двухкомпонентной структурой. Такой подход к уравнению Клейна – Гордона отличается от общепринятого [3] тем, что, при наличии аксиального поля, уравнение (21) позволяет рассматривать частицы со спином. 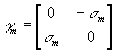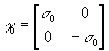Кроме того, факторизуя уравнения (1) и (10) с помощью матриц (, ) и преобразования типа (11), приходим к уравнениям Дирака для свободной частицы и для частицы в электромагнитном поле.

Литература:

1. Бьёркен, Дж.Д. Релятивистская квантовая теория. Т.2. Релятивистские квантовые поля [Текст]: моногр.; пер. с англ. / Дж.Д. Бьёркен, С.Д. Дрелл. – М.: Наука, 1978. – 408 с.

2. Елютин, П.В. Квантовая механика [Текст]: уч. пособие для физич. специальностей вузов / П.В. Елютин, В.Д. Кривченков. – М: Наука, 1978. – 336 с.

3. Хелзен, Ф. Кварки и лептоны [Текст]: моногр.; пер. с англ. / Ф. Хелзен, А. Мартин. – М.: Мир, 1987. – 456 с.

4. Бьёркен, Дж.Д. Релятивистская квантовая теория. Т.1. Релятивистские квантовые поля [Текст]: моногр.; пер. с англ. / Дж.Д. Бьёркен, С.Д. Дрелл. – М.: Наука, 1978. – 296 с.

5. Румер, Ю.Б. Теория групп и квантовые поля [Текст]: моногр. / Ю.Б. Румер, А.И. Фет. – М.: Наука, 1977. – 248 с.

6. Кейн, Г. Современная физика элементарных частиц [Текст]: моногр.; пер. с англ. / Г. Кейн. – М.: Мир, 1990. – 360 с.