К.т.н. Гнусов Ю.В., Кубрак В.П.

      Харьковский национальный университет внутренних дел

МОДЕЛИ БОКСА-ДЖЕНКИНСА В ПРОГНОЗИРОВАНИИ ПРЕСТУПНОСТИ

 

 

При прогнозировании преступности нам  чаще  всего  приходится иметь  дело  с  сильно  колеблющимися   временными   рядами.  При использовании полиномиальных предикторов для  сильно  колеблющихся рядов сглаживаются колебания, учет которых  может  быть  необходим для  правильного  принятия  решений.  В таких ситуациях для прогнозирования целесообразно применять методы, в которых прогноз ведётся не изолировано по тренду и случайной  компоненте, а в рамках объединенной модели. Адекватным методом для решения  такого рода задач является метод Бокса-Дженкинса.

Поскольку прогнозирование осуществляется на основе ретроспективных  данных,  очевидно,  что  внутри  временного  ряда существует  связь  между  отдельными его членами. Эта связь количественно выражается    автокорреляционной    и  частной корреляционной  функцией  ряда,  которые  будут  служить  основным инструментом при построении предикторов Бокса-Дженкинса.

Для построения моделей предварительно необходимо ввести в рассмотрение следующие операторы:

·     оператор сдвига назад, определяемый как BX[n]=X[n-1], отсюда BmX[n]=X[n-m] ;

·     оператор сдвига вперед, определяемый как EX[n]=X[n+1] ;  

·     разностный  оператор со сдвигом  назад,  определяемый   как DX[n]=X[n]-X[n-1]= (1-B)X[n],  то есть D=1-B=E+1.

Введенным  операторам  можно придать качественный статистический смысл. Так, например, широко применяемый при анализе преступности показатель темпа роста может быть определен как t = X[n+1]/X[n]  или X[n+1]=tX[n]  и  может  быть  отождествлен   с оператором E. Показатель темпа прироста может быть определен как

                               

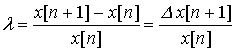
то есть связан с разностным оператором. Легко проследить связь  между темпом роста и темпом прироста

                   

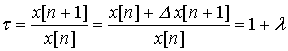
Для построения предиктора в рамках теории Бокса-Дженкинса используются следующие типы моделей:

·     авторегрессии (АР),

·     скользящего среднего (СС),

·     смешанные модели авторегрессии скользящего среднего (АРСС),

·     смешанные   модели    авторегрессии   проинтегрированного  скользящего среднего (АРПСС).

В моделях авторегрессии текущее значение процесса  выражается через предыдущие его значения и случайный импульс x[n]. Если  из процесса  временно  исключить  постоянную  составляющую  m,   то есть , то модель авторегрессии записывается

        

или                                                                        

где j(B)=1-j1(B)-j2(B)2 -...-jp(B)p. Чтобы  построить  такой  предиктор,    необходимо    отыскать    p+2     неизвестных    параметра: m, j1  ,..., jp , sx 2 , где sx 2  - дисперсия  «белого  шума» x. Заметим,  что  в  практике социально-экономических исследований  наибольшее  распространение получили  именно  модели авторегрессии. Модели авторегрессионного типа легко интерпретируются, ибо нетрудно представить  себе  ситуацию,  когда текущее значение  переменной  зависит  от  одного  или  нескольких предыдущих.

В  отличие  от  модели  авторегрессии, модель скользящего среднего  использует  некоторое  число  q предыдущих  значений случайных импульсов.

Предиктор имеет вид:

или                                                                         

где a(B)=1-a1(B)-a2(B)2 -...-aq(B)q. В этой модели неизвестными  являются q+2 параметра.

Если объединить эти две модели, то получим смешанную модель авторегрессии скользящего среднего:

или                                                                 

здесь уже p+q+2 неизвестных параметра.

В  том  случае,  если  исследуемый временной ряд проявляет явную нестационарность  (а это наиболее часто встречающийся  на  практике случай), его удобно представить обобщенным оператором авторегрессии F(B). В обобщенном операторе авторегрессии один или несколько нулей полинома F(B) (то есть один или несколько  корней  уравнения F(B)=0) равны единице. Оператор F(B) удобно записывать в виде

                                  

где j (B) - стационарный оператор авторегрессии.

При этом обобщенная  модель,  описывающая  нестационарный  процесс, имеет вид:

                 

или                                                              

где w[n]=Ddx[n]. Таким образом, нестационарный процесс мы  будем описывать предиктором, в котором  d-я  разность ряда (аналог производной непрерывного процесса)  является  стационарной. Здесь p+q+d+2 неизвестных, которые следует определить из наблюдений.

Исходной информацией для построения предиктора служат средние значения ряда, его  дисперсия  и автокорреляционная  функция. Их выборочные значения определяются следующими выражениями:

           

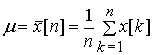
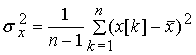
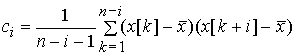,  i = 0, 1,...,m           .                                                

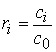Здесь m - среднее значение процесса, sx2 - его дисперсия, ci – автоковариационная функция, ri - автокорреляционная функция. Стационарность ряда проверяется по знакоопределенности автокорреляционной матрицы (матрицы Лорана)

     ,

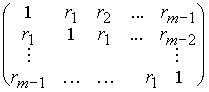которая для стационарных рядов является положительно определенной. На графике стационарному ряду соответствует быстро затухающая автокорреляционная функция.

Увязка моделей с данными лучше всего достигается процедурой, основанной на структурной идентификации и оценивании (параметрической  идентификации).

Заметим, что  в  настоящее  время  задачи  структурной  идентификации решаются в большинстве случаев на эвристическом уровне, что требует высокой теоретической  подготовки  и  опыта  решения практических задач у исследователя.  Использование ЭВМ для решения такого рода задач   ограничивается интерактивным  режимом, причем окончательное решение   принимает человек, что вносит значительный элемент субъективизма в  конечный результат. Полная автоматизация процесса структурной идентификации хотя и наталкивается на существенные трудности,  представляется весьма привлекательной. Один из возможных путей решения этой проблемы   состоит  в многократном  решении  задачи параметрической  идентификации   для   множества   возможных структур  и  выборе  наилучшей  из  моделей,  однако здесь результаты могут существенно отличаться в  зависимости  от применимых критериев идентификации и конкретных вычислительных процедур. Альтернативный подход к  решению этой проблемы состоит в использовании метода, основанного на теории распознавания образов. При этом  предполагается, что образ, соответствующий  конкретной  структуре, занимает конечный объем в пространстве признаков,   образованных коэффициентами  авто- и взаимокорреляционных функций. Сущность  подхода  состоит  в  нахождении   соответствующего разбиения  пространства  признаков  на основе информации, содержащейся в образах с  известной   классификацией. Разделяющие поверхности, построенные с использованием этих данных, используются в дальнейшем для классификации образов с неизвестной принадлежностью.

Рассмотрим  последовательность  этапов,   связанных   с решением  задачи  структурной  идентификации.   Пусть обобщенная модель задана  выражением

, тогда процесс идентификации состоит из:

·     определения порядка  взятия  разностей, необходимого для приведения процессов к стационарным;

·     определения структуры  фильтра для   выравнивания входных и выходных   последовательностей  (определения структуры процесса на входе);

·     определения чистого времени задержки между входным и выходным рядами;

·     определения порядка номиналов s(B) и w(B);

·     определения структуры модели случайного шума X.

Решение данных задач может быть проведено с помощью некоторой  системы распознания  образов  (она  может быть запрограммирована на ЭВМ), состоящей, как минимум, из трех основных подсистем: преобразователя, селектора признаков  и классификатора. Функция  преобразователя состоит в трансформации входного образа  (последовательностей  g[n], x[n]) в вектор признаков. Селектор признаков  последовательно выделяет  из  этого  вектора  признаки, существенные для построения разделяющих поверхностей.  Конкретное решение о принадлежности образа на основе информации,  содержащейся  в векторе  признаков,  применяется  последней  подсистемой   - классификатором.

Вектор образов формируется из коэффициентов авто- и частных  автокорреляционных  функций  входных и выходных последовательностей и из коэффициентов взаимокорреляционной функции. Существенные признаки выделяют из этого  вектора  с помощью   эвристических или математических    процедур. Эвристические процедуры базируются на знании отношений между образами и классами, в то время  как математические, методы базируются на оптимизации некоторого формального критерия разделимости классов. Классификация признаков представляет собой обучающуюся адаптивную систему, причем предполагается существование разделяющей поверхности  между  классами   в пространстве   признаков. Основная задача,  решаемая классификатором, состоит в нахождении неизвестных параметров этой поверхности.

Разработка  конкретной  распознающей системы основывается, как правило, на обучающей выборке  образов с известной классификацией. Процесс   обучения при этом рассматривается как разработка объективных  решающих  правил на основе информации, содержащейся в обучающей выборке, с помощью тех или иных математических средств.  Заметим, однако, что хорошо определенного формально решающего правила самого по  себе  недостаточно  для объективной структурной идентификации, поскольку надежность этих правил определяется надежностью  классификации  по  обучающей   выборке.   Таким образом, для того, чтобы исключить элемент субъективизма  из процесса  проектирования  распознающей  системы, обучающая выборка должна   генерироваться   имитационной  моделью, структура которой известна точно.

Первый и третий  этапы решения задачи структурной идентификации при таком подходе очень просты. В частности, подсистема, определяющая   необходимый  порядок взятия разностей для приведения исходных процессов  к стационарным представляет собой простейший двухклассовый  идентификатор, который  определяет  стационарность  либо   нестационарность предъявляемых последовательностей. При этом стационарность определяется с помощью авто- и взаимокорреляционной функции по Яглому либо по знакоопределенности матрицы Лорана. Если предъявляемые ряды нестационарны, то они дифференцируются и соответствующие коэффициенты корреляции опять   предъявляются  классификатору для  проверки на стационарность. Этот процесс повторяется до тех пор,  пока ряды не будут признаны стационарными.

Третий этап, на котором  определяется  задержка  между входом и выходом, реализуется с помощью простейшей пороговой функции. Задержка определяется номером первого коэффициента взаимной корреляции, который превышает заданный  порог. Как правило, эти этапы реализуются довольно просто и отличаются высокой надежностью решения.

Значительно более сложная проблема заключается в разработке решающего правила для решения задач идентификации выравнивающего фильтра (этап 2), передаточной функции  (этап 4),  модели  аддитивного  шума  (этап   5). Хотя   задачи, рассматриваемые на этих этапах, имеют различное качественное содержание,  решены они могут быть по однотипным вычислительным  схемам.  Данные схемы реализуют процедуры построения разделяющих  гиперповерхностей  для  конечного множества  классов. Казалось бы, что  задача определения множества возможных структур имеет бесчисленное  количество решений, однако,  как указывают Дж.Бокс и Г.Дженкинс,  в стохастических моделях порядок авторегрессии и скользящего среднего практически не превышает числа три. Таким образом, все возможные  структуры  образуют  15  различных  классов. Вектор  образов Z, как уже   указывалось, образуется коэффициентами авто- и частной  автокорреляционной  функции, т.е.

                        

Предположение о линейной разделимости классов сводит задачу распознавания образов к  задаче  определения  коэффициентов, задающих гиперплоскость C i , i = 1, 2, ...,15:

                                      

удовлетворяющих для любого Z из i-ого класса условию

                                  

Эта задача с вычислительной точки зрения не представляет никаких  трудностей,  основная  же  проблема  здесь - это формирование обучающих выборок для всех пятнадцати классов, что требует значительных затрат времени и средств.