Современные информационные технологии/2.
Вычислительная техника и программирование

Обідник М. Д.

Вінницький національний технічний університет

Концептуальні положення формування графічних зображень
високодеталізованих тривимірних сцен

Аналіз сучасного стану комп’ютерної графіки реального часу показав [1], що з кожним роком підвищується деталізація тривимірних сцен. Разом з тим, розміри полігонів, з яких складаються тривимірні моделі, зменшуються відносно площини екрану. Станом на кінець 2012 року в кадрі тестової сцени графічних прискорювачів серії Kepler у середньому налічується 4 мільйони полігонів при роздільній здатності 1920×1080 пікселів [2]. Таким чином, у середньому для високодеталізованих тривимірних сцен, кожен полігон на екрані користувача займає 10-50 пікселів. Така висока степінь деталізації досягається за рахунок адаптивної теселяції, що апаратно реалізується у графічних прискорювачах, які підтримують графічний стандарт DirectX 11.

Для коректного та реалістичного відображення градації кольорів на зображеннях поверхонь тривимірних полігональних об’єктів, у процесі розрахунку інтенсивності кольору, використовують складні моделі зафарбовування, що враховують всі три складові кольору – фонову, дифузну та дзеркальну (спекулярну) [3].

Сучасні графічні прискорювачі не в змозі у реальному часі відображати складні сцени з великою кількістю динамічних моделей, тому в графічних двигунах часто застосовуються спрощені методи формування зображень, наприклад зафарбовування Гуро. Хоча такий підхід і зменшує обчислювальні затрати на візуалізацію сцени, проте призводить до погіршення якості зображення та появи візуальних артефактів. Наприклад, при зафарбовуванні полігонів шляхом лінійної інтерполяції кольору, вникає ефект смуг Маха – коли в межах відблиску на гранях полігонів спостерігається візуальний ефект підвищення інтенсивності кольору. При підвищенні деталізації тривимірних об’єктів, цей ефект зводиться до мінімуму. Тому спрощені методи зафарбовування доцільно застосовувати для високодеталізованих поверхонь, тоді візуальна відмінність від зображень, побудованих за повними складними методами освітлення зводиться до мінімуму.

Підвищення деталізації тривимірних об’єктів призводить до зменшення розмірів полігонів та зменшення кутів між нормалями у вершинах полі-
гонів (рисунок 1), а також суттєвого збільшення кількості вертексних операцій. Оскільки формування вершин передбачає розрахунок їх ортогональних складових та нормалізацію векторів, виникає необхідність розробки спрощених векторних розрахунків.

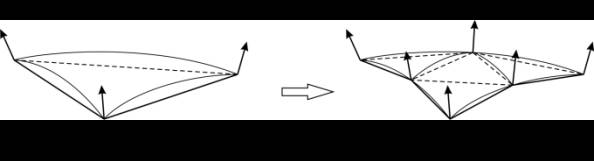
Рисунок 1. Підвищення деталізації полігональної сітки

Важливим параметром при зафарбовуванні є опуклість полігону, яка задається нормалями у вершинах. При цьому, чим більші кути між нормалями у вершинах полігону, тим більша його опуклість. При збільшенні деталізації тривимірних об’єктів кути між нормалями у вершинах полігонів зменшуються, що дозволяє зменшувати похибки обчислень для яких застосовуються спрощені розрахунки. Тому при застосуванні спрощених методів необхідно враховувати параметр кривизни полігону, який можна оцінити за величинами косинусів кутів між нормалями. Оскільки вони нормалізовані, то косинус між двома векторами можна знайти за формулою:

де і – нормалізовані вектори, а – косинус кута між ними.

Розміри полігонів на екрані комп’ютера залежать не тільки від деталізації тривимірного об’єкта, а й від його розміщення відносно спостерігача. При наближенні тривимірного об’єкта до точки спостереження збільшуються його розміри і, як наслідок, збільшуються розміри його складових полігонів. Щоб уникнути появи візуальних артефактів на зображенні, при формуванні якого застосовуються спрощені розрахунки, необхідно щоб розміри полігонів на екрані не перевищували певне значення. Для цього можна виконати додаткову тріангуляцію полігона вже на етапі растеризації [4].

Розміри полігонів на екрані користувача можна оцінити, перевіривши виконання нерівностей:

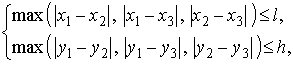
де , і – координати вершин полігону в екранному просторі, – максимально можлива ширина прямокутника, що обмежує полігон, а – його максимально можлива висота.

Отже, для того, щоб використовувати спрощені розрахунки, необхідно щоб сцена, спроектована у екранну систему координат, мала достатній рівень деталізації. Для приведення сцени до необхідного рівня деталізації необхідно, щоб розміри полігонів на екрані та кути між їх нормалями не перевищували певні задані величини. Для визначення відповідності рівня деталізації сцени до необхідного рівня (для того, щоб можна було використовувати спрощенні розрахунки) під час рендерингу використовуються порогові значення розмірів полігону і , а також порогове значення опуклості полігону , яке порівнюється з мінімальним значенням із трьох косинусів кутів, утворених нормалями трикутного полігону. У разі, якщо сцена не відповідає заданому рівню деталізації, виконується додаткова тріангуляція [4].

Важливою умовою рендерингу високодеталізованих сцен з використанням спрощених розрахунків є збереження достатньої якості формування графічних сцен. Тобто, візуальна відмінність між сформованим і еталонним зображеннями за повинна забезпечувати їх візуальну ідентичність [5].

Отже, найголовнішими концептуальними положеннями формування зображень високодеталізованих тривимірних сцен є:

1. Підвищення деталізації тривимірних сцен призводить до збільшення кількості вертексних операцій, суттєвого зменшення розмірів полігонів та кутів між векторами, що задають їх кривизну. Як наслідок, змешуються довжини ребер полігонів та рядків растеризації, що дає можливість спростити як програмну, так і апаратну реалізацію процесу рендерингу.

2. Збільшення рівня деталізації призводить до того, що суттєво збільшується відношення відстані від джерела світла до розміру полігона, що обумовлює сталість вектора напівшляху у його межах, а тому відпадає необхідність у визначенні цього вектора для кожної точки площини, обмеженої полігоном.

3. Оскільки кути між векторами, що задають кривизну полігону, зменшуються, то виникає можливість та необхідність розробки спрощених методів інтерполяції векторів, а також їх нормалізації. При цьому необхідно враховувати ступінь кривизни полігонів для того, щоб уникнути появи візуальних артефактів при застосуванні спрощених векторних розрахунків.

4. Для високодеталізованих поверхонь доцільно застосовувати методи адаптивного зафарбовування, що передбачають розрахунок спекулярної складової кольору тільки для тієї частини поверхні тривимірної моделі, де значення цієї складової не перевищує певний заданий поріг. Такі методи дозволяють уникнути надлишковості розрахунків спекулярної складової кольору у тих зонах, де її візуально не видно. Для реалізації такого адаптивного зафарбовування необхідна розробка методів ідентифікації відблисків.

5. Високий рівень деталізації тривимірних сцен дозволяє застосовувати спрощені методи перспективно-коректного розрахунку освітлення полігонів та перспективно-коректного накладання текстур.

6. Для використання спрощених розрахунків у процесі рендерингу необхідно привести тривимірну сцену до необхідного рівня деталізації, якого можна досягти, виконуючи, там де необхідно, додаткову тріангуляцію. Для цього доцільно застосовувати порогові значення розмірів полігонів в екранному просторі , і порогове значення опуклості полігону .

Джерела інформації:

1. Рысухин Р.П. Современное состояние и тенденции развития компьютерной графики // Волгоградский государственный аграрный университет. Волгоград, Россия. Электронный ресурс: http://www.scienceforum.ru/2013/pdf/3428.pdf.

2. Горбань П. Nvidia выпускает графическую демонстрацию Kepler // Новости Мир Nvidia. Электронный ресурс: http://nvworld.ru/news/nvidia-release-new-dawn-demo/.

3. Tomas Akenine-Möller. Real-Time Rendering / Tomas Akenine-Möller, Eric Haines, Naty Hoffman // 3rd edition, A. K. Peters Ltd., ISBN 978-1-56881-424-7, 2008, — 1045 pages. Электронный ресурс: http://www.real-timerendering.com.

4. Романюк О. Н. Методи додаткової тріангуляції / О. Н. Романюк, М. Д. Обідник // Вестник Херсонского национального технического университета. Вып. 3(42). – Херсон: ХНТУ. 2011. – С. 366 – 371.

5. Обідник М. Д. Аналіз методів оцінки якості графічних зображень / М. Д. Обідник, А. О. Стахов // Збірка матеріалів ІІ всеукраїнської науково- технічної конференції студентів, аспірантів та молодих вчених, 11-13 квітня 2011 р., м. Донецьк: зб. доп. у 2 т. / Донец. націонал. техн. ун-т; – Донецьк: ДонНТУ, 2011. - Т.2 262с.