Еркин Н.

Карагандинский государственный университет имени Е.А Букетова, Казахстан

Функции ограниченной p-вариации и класс Бесова

Определение: периодическая функция определенная на называется ограниченной p-вариации если такое, что для всех выполняется неравенства

.

Полной p-вариацией функции называется величина

,

.

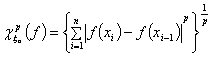Множество всех функции ограниченной p-вариации обозначается . В этом пространстве норма определяется по формуле

.

Определение:([2]). Дробным модулем непрерывности функции называется величина

.

Если , то

,

где, .

Определение:([2]). Пусть . Множества всех функции для которых

обозначается . Класс будет подпространством пространства с нормой .

Свойства модуля гладкости функции ограниченной p-вариации исследовал А.П. Терехин [2]. Теоремы теории приближения в пространстве доказали Б.И. Голубов [3], С.С. Волосивец [4].

Рассмотрим класс Бесова в пространстве .

Определение: Пусть . Если , и

,

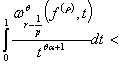
то будем говорить функция принадлежить классу .

Теорема: Пусть . Тогда класс будет полным нормированным пространством с нормой

Доказательство: Докажем, что нормированное пространство.

1. Очевидно, что.

Если , то . Поэтому , . Если , то . Следовательно

.

Поэтому .

2. Пусть. Так как нормированное пространство, то . По свойству конечной разности функции имеем

Поэтому по определению супремума

.

Если , то .

Поэтому,

Пусть. Тогда

Из этого неравенство равенства получим

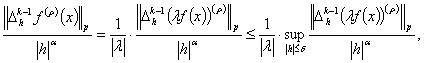
Теперь по определению супремума

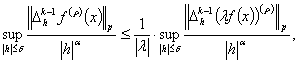
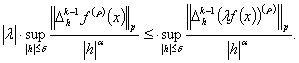
3. Пусть. Так как нормированное пространство, то . По свойству производной

По свойству конечной разности

Так как нормированное пространство, то

По определению супремума

Отсюда получим

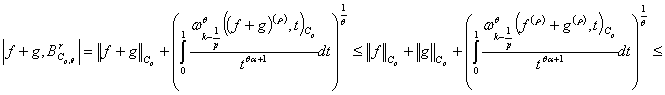
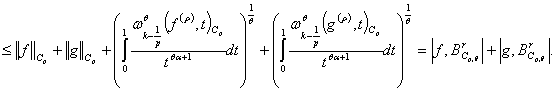
Литературы

1. Wiener N., The quadratic variation of function and its Fourier coefficients.

// Massachusett’s Jour.Mathematica, 1924., vol.3, p.72-94.

2. Терехин А.П., Приближение функций ограниченной вариации. Известия высших учебных заведений, Математика , 1965. №2 с.171-187.

3. Голубов Б.И., О наилучшем приближении абсолютно непрерывных функций. Изд-во Тбилисского унив-та.1988. с.85-99.

4. Волосивец С.С., Асимптотические характеристики одного компакта гладких функций в пространстве функций ограниченной вариации. Математические заметки, 1995, т. 57 с.214-227.