Иван Долгарев

ПРЯМОЙ ГЕЛИКОИД СРЕДИ ЕВКЛИДОВЫХ ПОВЕРХНОСТЕЙ.

Регулярная евклидова поверхность обладает евклидовыми и галилеевыми квадратичными формами, [1]. Во множестве регулярных евклидовых поверхностей выделяются замечательные поверхности, к ним относятся поверхности с постоянными коэффициентами галилеевых квадратичных форм. Это цилиндрические поверхности и прямой геликоид. В окрестности всякой обыкновенной точки, где постоянны коэффициенты галилеевых квадратичных, регулярная евклидова поверхность является либо областью цилиндрической поверхности, либо областью прямого геликоида.

1. Галилеевы квадратичные формы регулярной евклидовой поверхности

Общей основой евклидова пространства и пространства-времени Галилея является аффинное пространство. При введении скалярного произведения векторов в линейном пространстве аффинного пространства , аффинное пространство превращается в одно из евклидовых пространств, или в пространство-время Галилея. Ниже рассматривается 3-мерное пространство . Пусть = базис линейного пространства . Зная координаты векторов в базисе , можно получить координаты векторов в любом базисе. Пусть = и = произвольные векторы. Евклидовым скалярным произведением векторов , называется число

= ;

галилеевым скалярным произведением векторов , называется число

=

см. [2, с. 46 – 47]. Евклидовой нормой (модулем) вектора называется

= ,

галилеевой нормой вектора называется

=

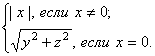
В результате получается соответственно, евклидово векторное пространство и аффинное пространство превратилось в евклидово пространство , или получается галилеево векторное пространство и аффинное пространство превратилось в пространство-время Галилея , т.е. галилеево пространство.

В аффинном пространстве определены кривые и поверхности. Кривая задается векторной функцией одного параметра

= , ;

поверхность задается функцией двух параметров

(1) = , .

Так как аффинное пространство может быть превращено и в евклидово пространство и в галилеево пространство , то все объекты аффинного пространства, в том числе кривые и поверхности, обладают и евклидовыми и галилеевыми свойствами; выявляются эти свойства в результате введения в линейное пространство соответствующего скалярного произведения векторов, [3]. Это означает, что существует единая геометрия пространства , она изучает аффинные свойства объектов, евклидовы свойства объектов, галилеевы свойства тех же объектов. Более того, для евклидовых объектов имеются галилеевы понятия. Для регулярной евклидовой кривой определены галилеева кривизна и галилеево кручение, [1]. Для регулярной евклидовой поверхности определены галилеевы квадратичные формы, [1, 3]. Галилеевы натуральные уравнения однозначно определяют евклидову кривую с точностью до положения, [4]. Коэффициенты галилеевых квадратичных форм однозначно определяют евклидову поверхность с точностью до положения. Галилеева определяемость евклидовых линий и поверхностей устанавливается гораздо проще, чем их евклидова определяемость.

Пусть регулярная евклидова поверхность задана в параметризации (1). Ввиду регулярности поверхности, хотя бы одна из покомпонентных функций (или все) обратима по параметрам , для определенности считаем, что для функции существует обратная по параметру функция . Следовательно, регулярная евклидова поверхность (1) обладает параметризацией

(2) = , .

Область в (2) может отличаться от области задания в параметризации (1). Параметризация (2) регулярной евклидовой поверхности называется выделенной. Далее рассматриваем евклидовы регулярные поверхности в выделенной параметризации.

Согласно [1], первой галилеевой квадратичной формой поверхности (2) называется

(3) = ,

где обозначено

(4) .

Единичным вектором галилеевой нормали поверхности (2) называется вектор

(5) = .

Векторы и взаимно перпендикулярны, но к линии вектор не перпендикулярен.

Второй галилеевой квадратичной формой регулярной евклидовой поверхности (2) называется

(6) = ,

ее коэффициенты таковы:

(7) , , .

Нормальная галилеева кривизна линии на евклидовой поверхности в направлении выражается функцией

.

Полная галилеева кривизна поверхности (2) равна

(8) .

2. О поверхности в пространстве Галилея

Напомним, что регулярная галилеева поверхность в естественной параметризации задается галилеевой векторной функцией

= , ;

смысл параметра есть время, параметр имеет пространственный смысл. Ее первая квадратичная форма есть

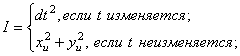
здесь и . Первая квадратичная форма галилеевой поверхности имеет вид галилеевой нормы векторов, см. выше, п.1. Вторая квадратичная форма галилеевой поверхности задается равенством (6), где заманено на и соответственно заменены символы производных второго порядка на и т.д. Формулы (3) – (8) написаны по соответствующим формулам галилеевой теории поверхностей применительно к евклидовым поверхностям. Полная кривизна поверхности выражена через коэффициент ее первой квадратичной формы и его производные:

,

см. [2, с. 94]. Формула верна для галилеевой полной кривизны регулярной евклидовой поверхности, т.к. она получена на основе коэффициентов (4), (7) и вектора галилеевой нормали (5).

3. Основная теорема теории поверхностей

Для регулярных евклидовых поверхностей доказана теорема Петерсона-Бонне о том, что поверхность однозначно, с точностью до положения, определяется заданием коэффициентов ее первой и второй квадратичных форм. Это основная терема классической евклидовой теории поверхностей. Доказательство основной теоремы настолько трудное, что в учебных курсах евклидовой геометрии не приводится. Использование галилеевых методов в евклидовой дифференциальной геометрии позволило получить очень простое доказательство основных теорем теории кривых, [1], и теории поверхностей, [4]. Евклидова кривая однозначно определяется своими галилеевыми кривизнами, регулярная евклидова поверхность однозначно определяется коэффициентами своих галилеевых квадратичных форм. Но ранее доказана основная теорема теории галилеевых поверхностей, [5]. По вычислительным формулам (4) и (7) коэффициентов квадратичных форм галилеевой поверхности получена система дифференциальных уравнений с частными производными, содержащая производные компонент функции и коэффициенты (4), (7) галилеевых квадратичных форм (3), (6) поверхности и вектора (5):

(9)

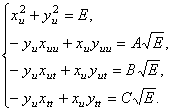
ОСНОВНАЯ ТЕОРЕМА галилеевой теории поверхностей, [4]. Если на односвязной области евклидовой плоскости заданы класса функции , , , – коэффициенты первой и второй квадратичных форм поверхности , то компоненты галилеевой поверхности являются решением системы дифференциальных уравнений с частными производными (9). Начальные условия вида , , , , , определяют единственную поверхность, проходящую через точку и имеющую векторы касательных , . Коэффициенты квадратичных форм найденной поверхности совпадают с заданными. [4 и 5].

4. Евклидовы поверхности, у которых постоянны

коэффициенты галилеевых квадратичных форм

Важным является случай, в котором коэффициенты галилеевых квадратичных форм регулярной евклидовой поверхности постоянны. В соответствии с (8), в этом случае постоянна полная галилеева кривизна евклидовой поверхности. Выявляется своеобразие евклидовой поверхности: прямого геликоида. Это поверхность ненулевой полной постоянной галилеевой кривизны.

Ниже полностью рассматриваются регулярные евклидовы поверхности с постоянным коэффициентами галилеевых квадратичных форм. Этим завершается изучение евклидовых поверхностей с таким свойством. В [4, 5] для постоянных найдены цилиндрические поверхности галилеева пространства

= , ,

функция, задающая евклидову поверхность отличается от лишь обозначением; функция, задающая евклидову поверхность, обозначается , . Укажем решение системы уравнений (9) при постоянных и .

Согласно (8), все рассматриваемые евклидовы поверхности имеют постоянную полную галилееву кривизну.

1. ТЕОРЕМА. Если на односвязной области евклидовой плоскости заданы постоянные величины

,

то на этой области определяется прямой геликоид

(10) = ,

коэффициенты первой и второй галилеевых квадратичных форм которого равны заданным величинам. Начальные условия

_,

определяют единственный геликоид, содержащий точку и имеющий касательную плоскость, натянутую на векторы .

Используется схема доказательства основной теоремы для евклидовых поверхностей с галилеевыми квадратичными формами. По виду первого уравнения системы (9) вводятся функции

(11) , .

Производные неизвестной функции отыскиваются по второму и третьему уравнениям системы (9): , , а функция находится как решение уравнения . Введенные функции интегрируются по параметру , что дает функции с точностью до слагаемых, зависящих от параметра . Эти слагаемые отыскиваются на основе четвертого уравнения системы (9), [4, 5].

# Рассматриваем функции (11), находим их производные

, , , .

По второму уравнению системы (9),

и по третьему уравнению системы (9):

.

Следовательно,

, .

Решением уравнения является функция

.

Функции (11) принимают вид:

, .

Находим:

= , .

Найденные функции дважды дифференцируем по параметру :

= , = .

Воспользуемся четвертым уравнением системы (10):

,

или окончательно

.

Две неизвестные функции связаны одним соотношением, одну из функций можно выбрать произвольно, считаем , остается равенство

(12) .

Если , то . В этом случае , . Указанные начальные условия выделяют прямой геликоид (10). Так как по условию коэффициенты квадратичных форм поверхности постоянны, то другие решения уравнения (12) неприемлемы. #

2. ТЕОРЕМА. Поверхность с коэффициентами и постоянной галилеевой кривизной не существует.

# Согласно общей схеме получения евклидовой поверхности по заданным коэффициентам ее галилеевых квадратичных форм, имеем в соответствии с (11)

, .

Находим функции

= , .

Дифференцируем их дважды по параметру :

.

По четвертому уравнению системы (9) имеем

,

окончательно: . При постоянном ненулевом равенство невозможно, следовательно, не существует поверхности с рассматриваемыми условиями. #

Найдены все регулярные евклидовы поверхности, коэффициенты галилеевых квадратичных форм которых постоянны. Справедлива следующая

3. ТЕОРЕМА. Пусть коэффициенты галилеевых квадратичных форм регулярной евклидовой поверхности постоянны. Если полная галилеева кривизна евклидовой поверхности равна нулю, то поверхность является цилиндрической

= , .

Если полная галилеева кривизна евклидовой поверхности отлична от нуля, , то поверхность является прямым геликоидом

= .#

По результатам исследования регулярных евклидовых поверхностей, имеющих постоянные коэффициенты галилеевых квадратичных форм, получаем такое утверждение.

4. ТЕОРЕМА. Единственной евклидовой поверхностью постоянной ненулевой полной галилеевой кривизны является прямой геликоид; его полная галилеева кривизна отрицательна, коэффициенты галилеевых квадратичных форм постоянны. #

В этом состоит уникальность прямого геликоида.

Использованная литература

1. Долгарев И. А., Долгарев А.И. Некоторые приложения галилеевых методов. // Известия высших учебных заведений. Поволжский регион. Физико-математические науки, - 2009, № 2(9), С. 39 – 59.

2. Долгарев А. И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.

3. Долгарев А. И. О геометрии 3-мерного действительного многообразия. // Вестник Татарского государственного гуманитарно-педагогического университета. – Казань, 2010, вып. 1(23). – С. 2 – 19.

4. Долгарев И. А. Системы дифференциальных уравнений в частных производных для поверхностей пространства Галилея: дис. … канд. физ.-мат. наук. - Пенза: ПГУ, 2007. – 119с.

5. Долгарев И. А. Нахождение поверхности в пространстве Галилея по ее квадратичным формам.// Известия высших учебных заведений. Поволжский регион. – 2006, № 5(26), С. 51 – 60. - (Естественные науки).