Математика/5.Математическое
моделирование
G. Mahambetova,
A.
Baimankulov
Kostanai State University
named after A. Baitursynov, Kazakhstan
NUMERICAL CALCULATIONS OF THE INVERSE TASK FOR FINDING
OF THE THERMAL
CONDUCTIVITY COEFFICIENT UNIFORM PRIMING
In this paper we study
one-dimensional problem of heat propagation in the soil. In general, any
problem of heat propagation is three-dimensional, but if the width and length
of the region are large enough, and the surface of this region is almost flat,
then the gradient of the horizontal distribution of heat is almost zero. In
this case, instead of three-dimensional problem can be studied one-dimensional
problem.
1 Statement of the Problem. Let in the area ![]() occurs heat
distribution under the influence of
the ambient temperature, in this case - the air. It is required
define of the thermal conductivity coefficient
occurs heat
distribution under the influence of
the ambient temperature, in this case - the air. It is required
define of the thermal conductivity coefficient ![]() . Decision of the task shall
search for from minimum functional
. Decision of the task shall
search for from minimum functional 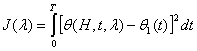 . Here
. Here ![]() computable meaning of the
temperature of the priming on surface of the land, but
computable meaning of the
temperature of the priming on surface of the land, but ![]() actual temperature of the priming on surfaces of the land. After theoretical discourses in work [9] is
received follow algorithm of the decision of the deliver task: 1) Is assigned initial approach
actual temperature of the priming on surfaces of the land. After theoretical discourses in work [9] is
received follow algorithm of the decision of the deliver task: 1) Is assigned initial approach ![]() ; 2) Dares straight line a task
; 2) Dares straight line a task 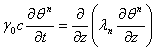 ,
, 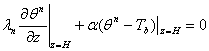 ,
, ![]() ,
, ![]() and is defined
and is defined ![]() and
and ![]() ; 3) Dares inverse task
; 3) Dares inverse task 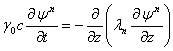 ,
, ![]() ,
, ![]() ,
, ![]() and is defined
and is defined ![]() ; 4) Is calculating gradient functional
; 4) Is calculating gradient functional 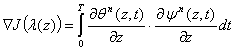 ; 5) Following approximation the thermal
conductivity coefficient is defined on
formula:
; 5) Following approximation the thermal
conductivity coefficient is defined on
formula: ![]() ,
, ![]() .
.
2 A numerical experiment.
For audit of validity received theoretical result is
organized numerical experiment. Studied uniform priming with data ![]()
![]()
![]() . Temperature surrounding
ambiences
. Temperature surrounding
ambiences ![]() , the thickness of the priming 5
m.; the step on time 0.5 hour; step on
spatial variable 0.001 m.
, the thickness of the priming 5
m.; the step on time 0.5 hour; step on
spatial variable 0.001 m.
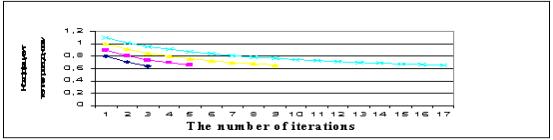
Figure
1. The track record to convergence iterations process. Initial approximation the thermal
conductivity coefficient ![]() .
.
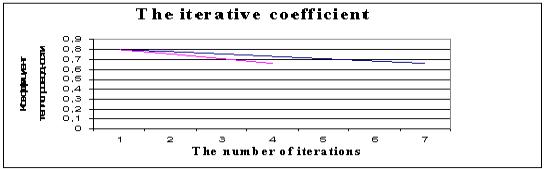
Figure
2. The Influence iterations coefficient ![]() . Initial approximation the thermal conductivity
coefficient
. Initial approximation the thermal conductivity
coefficient ![]() .
.
References:
1.
A.F.Chudnovsky (1976). Thermo
physics of the soil (pp.352). Moscow: Science.
2. A.Franchuk (1941). Thermal conductivity of construction
materials depending on the humidity. Gosstroizdat.
3.
B.Rysbaiuly& T.Akyshev(
2008). The approximate method of
determining the coefficient of heat transfer. The proceedings of International
Conference on mathematical methods in geophysics "ММG-2008". Russia,
Novosibirsk, Akademgorodok, 13-15 October.