Долгарев А.И.
СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ ПЕРВОГО ПОРЯДКА
В ЧАСТНЫХ ПРОИЗВОДНЫХ.
ЗАДАНИЕ ЕВКЛИДОВОЙ ПОВЕРХНОСТИ КОЭФФИЦИЕНТАМИ
ЕЕ ПЕРВОЙ КВАДРАТИЧНОЙ ФОРМЫ
Система двух линейных дифференциальных уравнений в частных производных сведена к уравнению в полных дифференциалах. На этой основе установлено, что регулярная евклидова поверхность однозначно, с точностью до положения, определяется коэффициентами только первой квадратичной формы.
1. Явно заданная поверхность
Регулярная евклидова поверхность может быть задана явной функцией
(1) 
, 
.
Векторное задание той же поверхности есть
(2) 
= 
.
Коэффициенты первой квадратичной формы поверхности
вычисляются по формулам
(3) 
, 
, 
.
Для функции (2) вычисляем:
(4) 
, 
.
В рассматриваемом случае
(5) 
, 
.
Знаки перед радикалами
определяются по второму коэффициенту 
; при 
в обыкновенной точке 
в области 
определения функции 
знаки производных
одинаковы, при 
знаки производных
противоположны. Возможны следующие векторы, определяющие касательную плоскость
в точке 
поверхности (1):
, 
,
где 
, 
. Плоскости 
, 
и также плоскости 
, 
симметричны
относительно координатной плоскости 
, т.е. определены с точностью до положения в пространстве.
Тем самым и поверхность (1) определяется с точностью до положения.
2. Система линейных уравнений в частных производных
и уравнение в полных дифференциалах
Для частных производных функции (1) имеем систему линейных дифференциальных уравнений в частных производных
(6) 
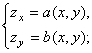
функция 
является решением
этой системы.
1. ЛЕММА.
Функция 
отыскивается как решение системы линейных
дифференциальных уравнений в частных производных первого порядка
(6), где 
, 
заданные дифференцируемые функции на некоторой односвязной области 
евклидовой плоскости, если система (6) совместна, т.е. выполняется равенство
(7) 
.
Начальные условия
определяют единственную функцию на области 
, являющуюся частным
решением системы уравнений (6). Системе
(6) соответствует уравнение в полных
дифференциалах
(8) 
с тем же множеством решений, что и система уравнений (6).
(Согласно
[1, с.335 – 336], условия Коши выделяют единственную поверхность 
из множества
поверхностей, составляющих общее решение системы уравнений (6). Значения 
, 
определяют угловые
коэффициенты касательных к поверхности.)
#
Если 
решение системы
уравнений (6), то имеется полный
дифференциал функции 
: 
и функция 
является решением уравнения
(8). Равенство (7) есть условие
интегрируемости уравнения (8) и системы уравнений (6). Всякое решение уравнения
(8) есть решение системы (6). Начальные условия выделяют частное решение
системы (6). #
Заметим, что линейному уравнению первого порядка в частных производных
соответствует, согласно [1, с. 338], система обыкновенных дифференциальных уравнений
.
Решение последней системы есть решение заданного уравнения в частных производных. В доказательстве леммы системе уравнений в частных производных соответствует уравнение в полных дифференциалах и не того вида, как в [1].
3. Отыскание явно заданной поверхности
по коэффициентам ее первой квадратичной формы
2. ТЕОРЕМА. Если
на односвязной области 
евклидовой плоскости заданы действительные дифференцируемые функции
двух действительных аргументов
(9) 
,
удовлетворяющие условиям
(10) 
,
то на этой области определяется поверхность (1) с точностью до положения в пространстве, для которой функции (9) являются коэффициентами первой квадратичной формы. Начальные условия
,
выделяют единственную поверхность, проходящую через точку 
и имеющую в этой точке касательную плоскость
(11) 
, 
, 
.
# Обозначим
(12) 
, 
;
знаки функций 
выбираем так, чтобы
(13) 
.
Имеем систему уравнений вида (6):
(14) 
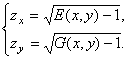
По первому из условий (10), 
, знаки радикалов выбираем по второму условию в (10). Согласно
лемме 1, системе уравнений (14) соответствует дифференциальное уравнение в
полных дифференциалах
,
удовлетворяющее условию интегрируемости в (10). Решение уравнения существует, обозначим его
(15) 
, 
.
Согласно (14), первая квадратичная форма каждой из поверхностей (15) имеет коэффициенты (9). Заданные начальные условия из семейства (15) выделяют единственную поверхность с касательной плоскостью (11). #
4. Параболоиды
Эллиптический и гиперболический параболоиды задаются функцией
.
Имеем в результате дифференцирования 
; коэффициенты первой квадратичной формы поверхностей есть
.
Отсюда по (5) находим
.
По коэффициенту 
видно, что
производные 
имеют знаки координат
обыкновенной точки,
или противоположны этим знакам. Сначала
рассмотрим случай
.
Уравнение 
имеет решение 
. Условие 
выделяет
эллиптический параболоид 
. В случае
, 
имеем гиперболический параболоид 
. В случаях 
и 
имеем те же
поверхности, но симметричные полученным, т.е. поверхности получены с точностью
до положения в пространстве.
5. Случай регулярной евклидовой поверхности,
заданной в общей параметризации
Пусть регулярная евклидова поверхность задана в параметризации
= 
, 
.
В учебниках евклидовой
дифференциальной геометрии отмечается, что регулярная поверхность 
задается и явной
функцией 
в окрестности всякой
своей обыкновенной точки. См., например, [2, с. 72 – 73, доказательство теоремы
1] и
[3, с. 209 – 211]. Согласно сказанному, имеют место
3.
ТЕОРЕМА. В окрестности всякой
обыкновенной точки регулярная евклидова поверхность задается явной функцией
. #
4. ТЕОРЕМА. (основная теорема евклидовой теории поверхностей) Всякая регулярная евклидова поверхность однозначно, с точностью до положения, определяется коэффициентами своей первой квадратичной формы.
#
В каждой обыкновенной точке регулярная евклидова поверхность описывается явной
функцией 
, теорема 3, а явно заданная поверхность с точностью до положения
определяется коэффициентами своей первой квадратичной формы, теорема 2. #
6. Задание полусферы
Сфера может быть задана параметрическими уравнениями
,
или неявной функцией
.
Ввиду 
, явное задание всей поверхности невозможно, рассмотрим
верхнюю полусферу
.
Находим
, 
.
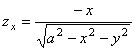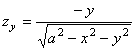Коэффициенты первой квадратичной формы полусферы таковы:
, 
, 
.
Система уравнений с частными производными (14) принимает вид
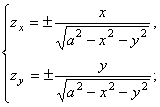
Согласно правым частям уравнений
следует считать, что 
, в противном случае поверхность будет задаваться функцией
комплексных переменных. Отыскиваем поверхность, задаваемую функцией 
. По виду коэффициента 
заключаем, что в
уравнениях системы координаты 
точек из области
задания поверхности 
могут быть взяты со
своими знаками или с противоположными. Возьмем противоположные знаки. По лемме,
имеем уравнение
,
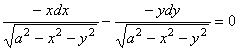его решение есть множество функций
.
Выбрав начальные условия 
; получаем верхнюю полусферу с центром в начале координат. Если
знаки для производных 
совпадают со знаками
координат 
, получаем нижнюю полусферу, т.е. ту же поверхность, что и
выше, с точностью до симметрии относительно плоскости 
.
7. Задание прямого геликоида
Прямой
геликоид описывается векторной функцией 
= 
и явной функцией
, 
,
см. [4, с. 323]. Имеем:
, 
.
Коэффициенты первой квадратичной формы геликоида есть
, 
, 
.
Знаки коэффициента 
можно истолковать
так, что знаки для производных 
следует выбирать противоположными.
Система (14) принимает вид
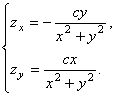
Согласно лемме, решая уравнение 
, находим
.
Зная 
, получаем 
= const. Начальные условия 
, выделяют поверхность 
.
8. Следствие факта наличия формулы Гаусса
для полной кривизны евклидовой регулярной поверхности
Здесь подразумевается формула Гаусса, выражающая полную кривизну евклидовой поверхности через коэффициенты первой квадратичной формы поверхности и ее производные. Вместе с тем, в евклидовой дифференциальной геометрии установлена теорема Петерсона-Бонне об определяемости регулярной евклидовой поверхности коэффициентами первой и второй квадратичных форм. Из приведенных фактов имеется следующее
5. СЛЕДСТВИЕ. Теорема 4 является следствием указанных в предыдущем абзаце фактов.
# По теореме Петерсона-Бонне с точностью до положения в пространстве регулярная евклидова поверхность определяется коэффициентами первой и второй квадратичных форм. В вычислительной формуле для полной кривизны поверхности
при доказательстве формулы Гаусса
величина 
выражена через
коэффициенты первой квадратично формы, см. например, [3, с. 348 - 349]. Это и
означает, что регулярная евклидова поверхность однозначно определяется
коэффициентами только ее первой квадратичной формы. #
Обсуждаемый факт евклидовой дифференциальной геометрии оставался незамеченным благодаря значительным трудностям в доказательстве основной теоремы теории поверхностей и в доказательстве формулы Гаусса. В учебниках по дифференциальной геометрии основная теорема теории поверхностей не доказывается, а только приводится в готовом виде и обсуждается важность теоремы. В связи с этим и не возникла постановка задачи о задании регулярной поверхности только коэффициентами первой квадратичной формы. Если не было задачи, то и могло быть ее решения. Указанная задача сформулирована и разрешена выше, в настоящей работе.
Заключение
Исследования, проведенные выше, показывают, что в отдельных случаях полезно использовать некоторые частные направления в исследованиях. Получена польза от того, что во всякой обыкновенной точке регулярной евклидовой поверхности эта поверхность может быть задана явной функцией. Как установлено выше, для определяемости поверхности достаточно задать только коэффициенты первой квадратичной формы.
Использованная литература
- Степанов В.В. Курс дифференциальных уравнений. - М., 1959. - 468 с.
- Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. - М.: Наука, 1979. - 560с.
- Рашевский П.К. Курс дифференциальной геометрии. – М.: Гостехиздат, 1956. 420с.
- Кривошапко С.Н., Иванов В.Н. Энциклопедия аналитических поверхностей. – Книжный дом «ЛИБРОКОМ», 2010. – 560 с.