Кесиян Г.А., Шахмеликян Т.А., Уртенов М.Х.

Кубанский государственный университет, Россия

Стохастическая модель краткосрочной торговли

В работе [2] была предложена модель финансового инструмента, учитывающая взаимосвязь цены, объема и открытого интереса:

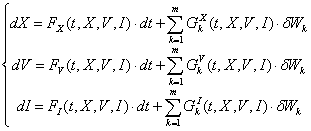, ₍₁₎

где δW – это бесконечно малый винеровский «шум», определяемый выражением , – это случайная величина, распределенная по нормальному закону распределения с нулевым математических ожиданием и единичной дисперсией (). При этом условную плотность распределения вероятностей состояния системы (1) можно найти из уравнения Фоккера — Планка (УФК) [1, 3].

При краткосрочной торговле, дейтрейдинге (интрадей), открытый интерес вряд ли принесет практическую пользу, потому что данные в отчетах идут с задержкой на несколько дней, а дейтрейдеру же нужна свежая информация по текущей сессии.

Следовательно, если не использовать лаговые переменные (задержка для открытого интереса), то можно допустить некоторые упрощения.

Таким образом, можно выдвинуть гипотезу, что в случае торговли в течение дня трейдеры не используют открытый интерес для формирования своих стратегий, поэтому открытый интерес не оказывает влияние на ценообразование в данном периоде. Тогда система (1) будет состоять из первых двух уравнений, а УФК будет определяться следующим выражением:

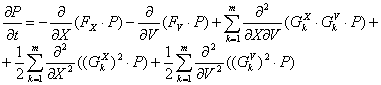
В работе [4] было установлено, что объем положительно коррелирует с абсолютным изменением цен. Эту зависимость мы учли в модификации процесса логарифмического блуждания следующим образом:

(2)

Выбор логарифмического блуждания как базовой модели можно объяснить его простотой при численном моделировании и идентификации параметров, наличием такой зависимости во многих системах, в том числе и в экономике, а также тем, что такой процесс во время блуждания никогда не опустится в область отрицательных значений, что характерно для цен.

Уравнение (2) мы будим использовать в качестве первого уравнения системы (1).

Графики объемов финансовых инструментов напоминают процесс, который притягивается к определенному уровню, вокруг которого совершает колебания в определенном интервале. Такое поведение можно описать с помощью процесса Орнштейна-Уленбека. Именно его мы и используем в качестве второго уравнения системы (1):

(3)

В уравнении (3) V притягивается к уровню, задаваемому константой α, при этом β определяет силу притяжения к указанному уровню.

На следующем рисунке продемонстрирован результат применения численной схемы Эйлера для процесса Оршнтейна-Уленбека в сочетании с исходными данными объемов двух финансовых инструментов:

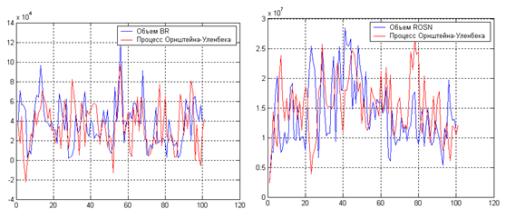
Моделирование объема с помощью процесса Орнштейна-Уленбека

На левом графике рисунка показан процесс Орнштейна-Уленбека для фьючерсного контракта на сырую нефть сорта Brent (BR), на правом – для акций ММВБ Роснефть (ROSN).

Таким образом, можно записать следующую стохастическую модель краткосрочной торговли:

(4)

Системе (4) соответствует следующее уравнение Фоккера — Планка:

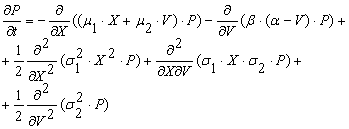
Имея условную плотность распределения вероятностей, можно вычислять среднее, волатильность, автокорреляционную функцию и другие характеристики случайного процесса.

Литература:

1. Гардинер К.В. Стохастические методы в естественных науках. М.: Мир, 1986.

2. Кесиян Г.А., Уртенов М.Х. Стохастическая модель финансового инструмента, учитывающая взаимосвязь цены, объема и открытого интереса : материалы международной научно-практической конференции, г. София, 17-25 февраля 2013 г. / София. - София : Изд-во ООД «Бял ГРАД-БГ», 2013. – 80 с. – ISBN 978-966-8736-05-6

3. Степанов С.С. [Электронный ресурс] // Стохастический мир : электрон. версия книги / Сергей С. Степанов. – [Б.м.], 2011. – С. 224-227. - URL: http://synset.com/pdf/ito.pdf.

4. Jiang Wang A Model of Competitive Stock Trading Volume / Journal of Political Economy - J POLIT ECON, vol. 102, no. 1, 1994