Математика / 5. Математическое моделирование

к.ф.-м. н. Калжанов М.У.

Костанайский государственный университет

имени А.Байтурсынова

Алгоритм укрупнения градаций признаков

Предположим, что признаку y, характеризующему объекты совокупности, соответствует разбиение , классы которого состоят из объектов, имеющих одно значение этого признака. Назовем укрупнением y разбиение совокупности , каждый класс которого суть объединения некоторого поднабора множеств r_α.

Значения номинальных признаков не упорядочены , поэтому допустимы любые укрупнения: классы разбиения R могут быть объединениями практически любого набора множеств r_α. Классы ранговых признаков упорядочены, поэтому допустимыми укрупнениями таких признаков будем считать разбиения, классы которых представимы в виде 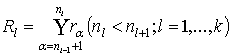. При укрупнении количественных признаков мы будем рассматривать их как ранговые, учитывая лишь порядок их значений; в конечном итоге разбиение R даст нам интервалы значений.

В зависимости от цели исследования качество укрупнения можно оценивать, используя подходящую вещественную целевую функцию Q(R), определенную на множестве допустимых разбиений совокупности объектов; при укрупнении стоит задача максимизации этой функции.

Обозначим , разбиение, полученное из R перемещением подмножества объектов r_α в класс R₁. Обычно относительно быстро (по сравнению с ) вычисляется величина приращения Q при таком изменении R: , этот факт используется в реализованных алгоритмах.

Итерация алгоритма укрепления номинального признака состоит в том, что поочередно рассматриваются классы исходного разбиения r_α (α = 1, …, n). При рассмотрении r_α отыскивается l, для которого величина максимальна, и при переходе к r_α+1 вместо R берется . Итерации повторяются до тех пор, пока есть положительные приращения , после чего улучшенное таким образом R принимается за искомое оптимальное укрупнение.

Рассмотрим алгоритм укрупнения ранговых признаков. Пусть . Обозначим R(β) разбиение, полученное из R_β заменой двух классов R_l и R_l+1 на 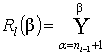и 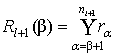, полагая Ø. В итерации алгоритма поочередно рассматриваются пары классов R_l и R_l+1 (l = 1, …, k). При рассмотрении R_l и R_l+1 отыскивается β, для которого величина Q(R(β)) максимальна (оптимальное β) и при переходе к следующей паре классов разбиение R заменяется на R(β). Итерации повторяются до тех пор, пока величина Q(R) увеличивается.

Рассмотрим, каким образом отыскивается оптимальное β. Прежде всего заметим, что безразлично, что максимизировать: Q(R(β)) или P(β) = Q(R(β)) - Q(R(n_l-1)). Для Р выполняется рекуррентное соотношение P(β) = P(β-1) + , с использованием которого последовательно вычисляются P(β) для β = п_l-1 + 1, …, n_l+1, в том числе и Р(п_l). Величина приращения Q при замене R на R(β) выражается следующим образом: Q(R(β)) - Q(R) = P(β) - Р(п_l).

Таким образом, отыскивая оптимальное β, мы одновременно получаем величину приращения при , мы узнаем, насколько увеличилась Q(R) в результате итерации.

Пусть - важные с точки зрения исследователя признаки. Знание значений признака у позволяет в той или иной мере предсказывать значения признаков системы Х. Укрупнение градаций признака у вызывает некоторое уменьшение точности такого прогноза, поэтому целью укрупнения является минимальная потеря информативности.

Для измерения степени информативности разбиения R по отношению к признаку х используется коэффициент Валлиса:

,

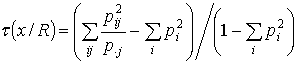где - доля объектов, имеющих i значение признака х и содержащихся в j-м классе R, и

В нашем случае необходима максимизация сразу для всех признаков . Одним из способов построения целевой функции в такой многоцелевой задаче является суммирование целевых функций:

.

Пусть группа объектов r_α, содержащая в классе j, переносится в класс l, тогда величина приращения выражается следующим образом:

,

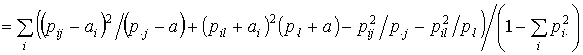где - доля объектов, имеющих i-е значение признака х и содержащихся в r_α, - доля объектов r_α в совокупности. Эта величина вычисляется

быстрее, чем , поскольку суммирование в правой части выражения производится только по одному индексу i, следовательно, использование приращения оправдано.

Литература :

1. Методы принятия технических решений : Пер. с нем.- Мушик Э., Мюллер П., М.: Мир, 1990. – 208 С.

2. Сборник задач по теории надежности .Половко А.М., Маликов И.М., Жигарев А.Н., Зарудный В.И. – М. : Советское радио , 1972 .- 408 С.