Математика / 5. Математическое моделирование

к.ф.-м. н. Калжанов М.У.

Костанайский государственный университет

имени А.Байтурсынова

Структуированный анализ информации

Предположим , система признаков описывает поведенческое характеристики , детерминирующие признаки. Для этих наборов можно построить матрицу коэффициентов зависимости признаков системы X от признаков системы Y. Результатом решения задачи должно быть разбиение системы и К разбиение матрицы , элементы которой имеют вид

В соответствии с идеологией аппроксимации ставится задача минимизации эвклидовой нормы разности матрицы А и В рассматриваемой как вектора в - мерном пространстве:

Нетрудно показать, что величина должна совпадать со средней величиной зависимости признаков системы от признаков системы .

.

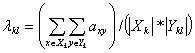Таким образом, при таком подходе минимизируется сумма квадратов отклонений величины коэффициентов от средних в подматрицах , величина характеризует степень детерминации признаков степени признаками системы .

Назовем типологией классификацию объектов, классы которой описываются в терминах значений признаков, характеризующих объекты. Данный пункт посвящен построению типологий с помощью метода последовательных разбиений совокупности объектов.

В зависимости от цели описанной процедуры построения классификаций можно выбрать вещественную функцию Q(R), определенную на множестве разбиений исходного материала объектов. Задача состоит в максимизации Q(R), иными словами, требуется найти , для которого показатель Q(R) был бы максимален.

Пусть имеется система признаков . Требуется построить разбиение, которое наиболее полно представляет, характеризует систему признаков X. Насколько хорошо разбиение R характеризует отдельный признак x, можно оценить, используя произвольный показатель зависимости признаков . В нашем случае необходима максимизация сразу для всех признаков . Одним из способов построения целевой функции в такой многоцелевой ситуации является суммирование целевых функций:

В реализованном нами алгоритме использован коэффициент Валлиса , т.е. использована целевая функция .

Методика работы с этим алгоритмом заключается в следующем. Прежде всего, определяется необходимая сложность типологии. Для этого исследователь строит гипотетическое дерево, оценивая, сможет ли он проанализировать его как результат работы ЭВМ. На основе одной иерархической группировки в реализации алгоритма можно строить несколько типологий, имеющих различное число классов (например, 2, 3, 5). Из них выбирается типология, более всего удовлетворяющая исследователя.

При описании полученной типологии, необходимо прежде всего выяснить, что представляют собой типы по отношению к системе X. Это можно узнать, сравнивая распределения признаков в различных типах полученной типологии. В результате обычно получаются упорядочения «лучший», «средний» и «худший» классы.

После этого, исходя из системы признаков Y, нужно проанализировать, какие объекты составляют полученные типы. При этом обычно возникают вопросы и гипотезы, почему те или иные группы объектов попали в тот или иной класс. Этот этап наиболее труден, однако он помогает установить любопытные закономерности.

Таким образом, у исследователя складывается представление о классификации с двух различных сторон, что в целом определяет связь между системами X и Y.

Рассмотрим частный случай, когда система состоит из единственного признака. Работа исследователя при анализе полученной типологии значительно упростится, если установить соответствие между значениями признака x и полученными типами. В этом случае можно сказать, что те или иные значения x описываются тем или иным типом объектов. Задачу построения такой типологии, где типы соответствуют значениям признака, будем называть задачей описания значений признака.

Для определения целевой функции в этой задаче рассмотрен простейший случай описания признака x признаком y. Допустим, что мы всем объектам совокупности присваиваем - е значение признака x. Вероятность правильного прогноза при этом будет ровна . При условии знания -го значения признакаэта вероятность ровна . Приращение этой вероятности обозначим .

Будем говорить что - е значение признака описывает - е значение признака , если . Иными словами, то, что - е значения _, означает, что вероятность правильного прогноза именно - й градации увеличилось максимально по сравнению с исходной вероятностью объектов; при укрупнении стоит задача максимизации этой функции. В частности, в нашей реализации целью является согласование укрупнения с заданным набором признаков , и в качестве целевой функции выбрана уже упомянутая

Литература :

1. Надежность и эффективность в технике : Справочник В 10 т. Т. 5 Проектный анализ отчетности / Под ред. В.И. Патрушева и А.И. Рембезы. М. Машиностроение , 1988.- 224 С.

2. Сборник задач по теории надежности .Половко А.М., Маликов И.М., Жигарев А.Н., Зарудный В.И. – М. : Советское радио , 1972 .- 408 С.