К.ф.-м.н. Е.А. Будылина,
Московский
государственный машиностроительный университет (МАМИ)
д.т.н.,
профессор А.М. Данилов, к.т.н.
А.Н. Круглова
Пензенский
государственный университет архитектуры и строительства
Тренажеры транспортных систем: оценка влияния
зоны нечувствительности и запаздывания
Рассматривается эргатическая транспортная система, техническая часть которой имеет
вид, приводимый на рис.1.

Рис. 1
Передаточная функция W(P) соответствует
линейной системе
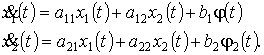
Определим зависимость выходных координат ![]() ,
, ![]() от параметров системы. Разобьем последнюю на
две подсистемы:
от параметров системы. Разобьем последнюю на
две подсистемы:
![]() ;
;
![]() .
.
Преобразование Р определяется запаздыванием и зоной
нечувствительности. Примем:![]() . Однородная часть системы (1) полностью определяется инвариантами
системы
. Однородная часть системы (1) полностью определяется инвариантами
системы ![]() ;
;![]() .
.
По
предыдущему получим:
![]() ,
,![]() ;
; ![]() ,
, ![]() .
.
Методом
вариации произвольных постоянных с учетом начальных условий, получим
представления ![]() ,
, ![]() через параметры
системы и входные воздействия:
через параметры
системы и входные воздействия:
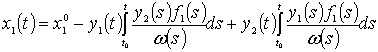 ,
,
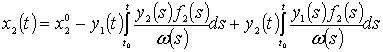 .
.
Вронскиан 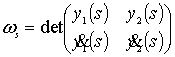 ;собственные функции
;собственные функции ![]() ,
, ![]() определяются по
характеристическому уравнению.
определяются по
характеристическому уравнению.
Отметим, в силу ![]() ,
, ![]() неизбежно возникает
вопрос о дифференцируемости входного
сигнала. Однако, на самом деле, в приведенных представлениях имеем интегралы
вида
неизбежно возникает
вопрос о дифференцируемости входного
сигнала. Однако, на самом деле, в приведенных представлениях имеем интегралы
вида ![]() с бесконечно
дифференцируемой функцией
с бесконечно
дифференцируемой функцией ![]() . Поэтому интегрируя по частям
. Поэтому интегрируя по частям
(![]() ), получим формулы, в которых отсутствуют производные функции
), получим формулы, в которых отсутствуют производные функции
![]() . Отсюда следует, что дифференцируемости входного сигнала
. Отсюда следует, что дифференцируемости входного сигнала ![]() не требуется.
не требуется.
![]() При двух различных действительных корнях
При двух различных действительных корнях ![]() ,
,![]()
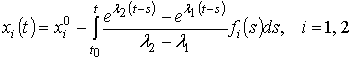 .
.
При
![]() имеем
имеем
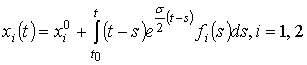 .
.
Наконец, при ![]() ,
, ![]() имеем:
имеем:
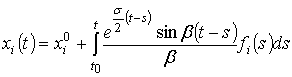 .
.
Если ![]() ,
, ![]() ,
, ![]() малы, то с учетом
малы, то с учетом 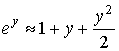 ,
, ![]() , приведенные формулы существенно упрощаются (для всех трех
случаев):
, приведенные формулы существенно упрощаются (для всех трех
случаев):
- при
линейной аппроксимации 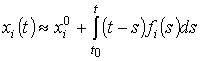 ;
;
- при квадратичной аппроксимации 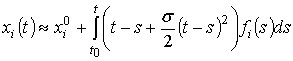
Так как реальные системы асимптотически
устойчивы (![]() ), то при больших
), то при больших ![]() множители
множители ![]() ,
, ![]() малы (малы и
подынтегральные выражения). Приведенные аппроксимационные формулы можно
использовать при решении многих прикладных задач (в частности, при разработке
имитатора динамики полета авиационного тренажера с учетом короткопериодической
составляющей продольного движения самолета).
малы (малы и
подынтегральные выражения). Приведенные аппроксимационные формулы можно
использовать при решении многих прикладных задач (в частности, при разработке
имитатора динамики полета авиационного тренажера с учетом короткопериодической
составляющей продольного движения самолета).
Количественный анализ влияния преобразования
Р на выходные координаты системы ![]() ,
, ![]() возможен лишь для
некоторых случаев. В частности, сравним выходные координаты двух систем:
возможен лишь для
некоторых случаев. В частности, сравним выходные координаты двух систем:
![]()
![]() ,
,
при входном сигнале
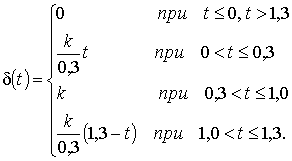
Для рассматриваемых здесь систем ![]() . Без ограничения общности можно принять начальные условия
нулевыми
. Без ограничения общности можно принять начальные условия
нулевыми ![]() .
.
При ![]() для первой системы имеем:
для первой системы имеем:
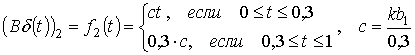 .
.
А для второй
системы:
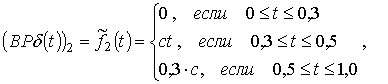 (принято
(принято ![]() ).
).
Используя аппроксимационные формулы, легко получить ![]() и
и ![]() , а также относительную варианту
, а также относительную варианту
 .
.
Зависимости координат ![]() от параметров матрицы
В легко просматриваются в самом общем виде. Это следует из того, что элементы
матрицы В являются коэффициентами в
выражениях для функций
от параметров матрицы
В легко просматриваются в самом общем виде. Это следует из того, что элементы
матрицы В являются коэффициентами в
выражениях для функций ![]() ,
, ![]() :
:
![]() ,
, ![]() .
(17)
.
(17)
Функции ![]() ,
, ![]() входят множителями в
формулы расчета
входят множителями в
формулы расчета ![]() ,
, ![]() (см. (10)-(14) при
нулевых начальных условиях). При
(см. (10)-(14) при
нулевых начальных условиях). При ![]() (напомним, что для
реальных систем рассматриваемого класса
(напомним, что для
реальных систем рассматриваемого класса ![]() ), то изменение коэффициента
), то изменение коэффициента ![]() на р% влечет изменение
на р% влечет изменение ![]() соответственно на р%.
соответственно на р%.
В заключение, определим зависимость выходных координат от
коэффициентов матрицы А. При линейной аппроксимации зависимость не
просматривается. При квадратичной аппроксимации ядра интегрального оператора в аппроксимационной
формуле видна зависимость от ![]() . Количественные
оценки легко получить для конкретных систем (конкретных вариаций
. Количественные
оценки легко получить для конкретных систем (конкретных вариаций ![]() ). В аппроксимационных формулах 3-го порядка видна
зависимость также и от
). В аппроксимационных формулах 3-го порядка видна
зависимость также и от ![]() . Так в случае действительных различных корней:
. Так в случае действительных различных корней:
 .
.
Таким образом, зависимость от ![]() и
и ![]() проявляется при
больших
проявляется при
больших ![]() . Множители
. Множители ![]() ,
, ![]() в интегралах – малы (реальные
системы устойчивы:
в интегралах – малы (реальные
системы устойчивы: ![]() ), поэтому зависимость
), поэтому зависимость ![]() от коэффициентов
матрицы А проявляется слабее.
от коэффициентов
матрицы А проявляется слабее.