А.И. Долгарев
НОВЫЙ ВИД ОСНОВНОЙ ТЕОРЕМЫ ГАУССА
В ЕВКЛИДОВОЙ ТЕОРИИ ПОВЕРХНОСТЕЙ
Известна теорема Гаусса о том, что полная кривизна евклидовой регулярной поверхности относится к ее внутренней геометрии; она выражается через коэффициенты первой квадратичной формы поверхности и производные первого и второго порядка этих коэффициентов, [1, с. 347]. Ниже приведено еще одно доказательство указанного факта, значительно более простое, чем известные, и простой аналог формулы Гаусса, который, к тому же, не содержит производных второго порядка.
1. Явно заданная евклидова поверхность
Евклидова регулярная поверхность может быть задана дважды дифференцируемой явной функцией
(1) ![]() ,
, ![]() .
.
Эту же поверхность можно задать векторной функцией
(2) ![]() =
= ![]() .
.
Производные векторной функции таковы
(3) ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Первая основная дифференциальная квадратичная форма поверхности (2) имеет вид
![]() ,
,
ее коэффициенты вычисляются по формулам
(4) ![]() ,
, ![]() ,
, ![]() .
.
Вторая основная дифференциальная квадратичная форма поверхности (2) есть
![]() ,
,
ее коэффициенты
(5) ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Полная, или Гауссова кривизна поверхности равна
(6) ![]() .
.
Используя значения производных
(3) и формулы коэффициентов (4), (5), имеем следующие выражения коэффициентов
первой и второй квадратичных форм поверхности (1) через производные функции ![]() .
.
(7) ![]() ,
, ![]() ,
, ![]() ;
;
(8) ![]() ,
, ![]() ,
, ![]() .
.
2. Формула Гаусса для явно заданной поверхности
1. ТЕОРЕМА. Для явно заданной поверхности (1) полная кривизна выражается через коэффициенты ее первой квадратичной формы и производные первого порядка этих коэффициентов и имеет вид
(9) ![]() .
.
# Коэффициенты второй квадратичной формы поверхности (1) выражены через производные второго порядка функции (1) и детерминант первой квадратичной формы поверхности, (8). Производные второго порядка функции (1) можно получить, дифференцируя формулы (7) для коэффициентов первой квадратичной формы поверхности (1).
По первой и третьей формулам в (7) имеем
![]() ,
, ![]() ,
,
отсюда, соответственно,
![]() ,
, 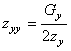 .
.
Подставляем найденные значения в первую и третью формулы в (8):
(10) ![]() ,
, 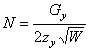 .
.
Снова по первой и второй формулам в (7) находим
![]() ,
, ![]() ,
,
откуда
![]() ,
, ![]() .
.
С учетом второй формулы из (7) имеем
![]() .
.
Вторая формула из (8) дает
(11) ![]() .
.
Найденные выражения (10) и (11)
коэффициентов второй квадратичной формы через коэффициенты первой квадратичной
формы поверхности подставляем в (6), применяем вторую формулу из (7) и получаем
(9). #
3. Полная
кривизна полусферы
Вычислим по (9) полную кривизну верхней полусферы
![]() ,
, ![]() .
.
Находим производные заданной функции
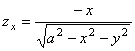 ,
, 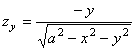 ;
;
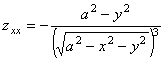 ,
, 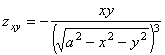 ,
, 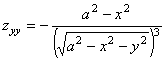 .
.
По (7) имеем значения коэффициентов первой квадратичной формы полусферы
![]() ,
, ![]() ,
, ![]() .
.
Находим детерминант первой квадратичной формы
![]() .
.
Вычисляем по (8) коэффициенты второй квадратичной формы полусферы
![]() ,
, ![]() ,
, ![]() .
.
Так как
![]() ,
,
то, по (6), полная кривизна полусферы равна
![]() .
.
Производные коэффициентов первой квадратичной формы полусферы таковы
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Согласно формуле (9), вычисляем:
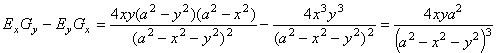 ,
,
![]() .
.
По формулам (6) и (9) получен один и тот же результат. Доказательство формулы (9) дано в п.2, в рассмотренном примере имеется подтверждение формулы (9) в частном случае.
4. О теореме Гаусса для регулярной поверхности, заданной векторной
функцией
Регулярная евклидова поверхность описывается векторной функцией
(12) ![]() =
= ![]() ,
, ![]() .
.
Считается, что область ![]() задания поверхности
принадлежит евклидовой плоскости, расположение этой плоскости в евклидовом
пространстве произвольно. В учебниках по дифференциальной евклидовой геометрии
отмечается, что от задания (12) регулярной поверхности можно перейти к неявному
заданию той же поверхности
задания поверхности
принадлежит евклидовой плоскости, расположение этой плоскости в евклидовом
пространстве произвольно. В учебниках по дифференциальной евклидовой геометрии
отмечается, что от задания (12) регулярной поверхности можно перейти к неявному
заданию той же поверхности ![]() ,
,
а это неявная функция для функции
![]()
переменной ![]() параметров
параметров ![]() , см., например, [1, с. 209 – 211] и [2, с. 72 – 73], существование
явного задания поверхности обеспечено регулярностью поверхности.
, см., например, [1, с. 209 – 211] и [2, с. 72 – 73], существование
явного задания поверхности обеспечено регулярностью поверхности.
Таким образом, имея векторно заданную регулярную поверхность, мы имеем ту же поверхность в явном задании. Теорема 1 устанавливает, что полная кривизна явно заданной поверхности относится к ее внутренней геометрии. Согласно приведенным выше рассуждениям, справедлива известная
2. ТЕОРЕМА. Независимо от способа задания, полная кривизна регулярной евклидовой поверхности относится к внутренней геометрии поверхности.
5. О порядке производных функции, задающей регулярную поверхность,
входящих в формулу Гаусса
В формулировке теоремы Гаусса в [1, с. 209] указано, что полная кривизна поверхности зависит и от производных первого и второго порядка коэффициентов первой дифференциальной формы регулярной поверхности.
3. ТЕРЕМА. Полная кривизна регулярной евклидовой поверхности зависит от коэффициентов первой квадратичной формы поверхности и производных первого порядка этих коэффициентов.
# Утверждение есть следствие вида формулы (9). #
Согласно формулам (6), (4) и (5), полная кривизна регулярной поверхности есть функция производных первого и второго порядков функции, задающей поверхность. Нет оснований ожидать, что порядки производных функции, задающей поверхность, повысятся в формуле Гаусса, выражающей полную кривизну поверхности только через коэффициенты ее первой квадратичной формы. Указанное свойство выполняется в формуле (9). Но в формуле Гаусса, приведенной в [3, с. 133],
(13) 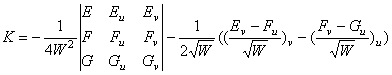 ,
,
это свойство нарушено. Формула содержит производные третьего порядка – производные от производных первого порядка коэффициентов первой квадратичной формы поверхности. Но указанная формула, тем не менее, может иметь место. Приведем пример поверхности, доказывающий неверность формулы (13) и исправим формулу.
Рассмотрим эллиптический параболоид
![]() =
= ![]() .
.
Производные первого порядка
функции ![]() :
: ![]() . Коэффициенты первой квадратичной формы параболоида:
. Коэффициенты первой квадратичной формы параболоида: ![]() . И находим производные коэффициентов:
. И находим производные коэффициентов: ![]() ,
, ![]() . Определитель первой квадратичной формы равен
. Определитель первой квадратичной формы равен ![]() . Вычислим входящий в (13) определитель.
. Вычислим входящий в (13) определитель.
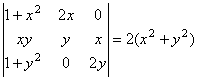 .
.
Находим:
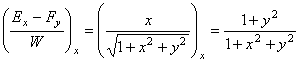 ;
; 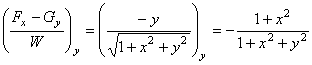 .
.
Теперь, по (13),
![]() -
- 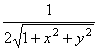
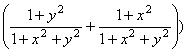 .
.
Возможно, в [3, с. 133] опечатка; в случае, если (13) исправить следующим образом:
(14) 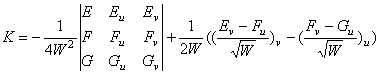 ,
,
получаем и по (13) и по (6) один
и тот же результат ![]() . Так дело обстоит в рассматриваемом примере, а как в общем
случае – неизвестно.
. Так дело обстоит в рассматриваемом примере, а как в общем
случае – неизвестно.
Теорема 3 верна; но есть случаи, например, формула (14), зависящие от способа доказательства формулы Гаусса, в которых полная (Гауссова) кривизна поверхности зависит только от коэффициентов ее первой квадратичной формы и производных первого и второго порядка этих коэффициентов.
Использованная литература.
- Рашевский П.К. Курс дифференциальной геометрии. – М.: Гостехиздат, 1956. 420с.
- Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геометрия. - М.: Наука, 1979. - 560с.
3. Позняк Э.Г., Шикин Е.В. Дифференциальная геометрия. – М.: Изд-во МГУ, 1990. – 384с.