Педагогические науки/5. Современные методы преподавания

Магистр тех. наук Трапезников Е.В., ст. гр. Ин(о)-10 Левицкий С.Л.

Северо-Казахстанский Государственный Университет им. М. Козыбаева, Петропавловск, Республика Казахстан

Методика проведения занятий по теме «Системы счисления» в рамках элективного курса для среднего звена

Систему счисления можно рассмотреть как формальные языки, имеющие алфавиты и позволяющие не только именовать объекты, но и выполнять над ними арифметические операции по определенным правилам.

На вводном занятии элективного курса учителю необходимо рассказать учащимся о важности изучения темы «Система счисления», а также что различная информация в памяти компьютера представлена в двоичной системе счисления и для внешнего представления содержимого памяти, адресов памяти используют шестнадцатеричную или восьмеричную.

Основные цели обучения систем счисления:

- дать представление о системах счисления;

- научить переводить числа в различные позиционные системы счисления;

- выполнять арифметические операции в различных системах счислениях;

- показать возможности использования двоичной системы счисления.

С методической точки зрения бывает очень эффектным прием, когда учитель подводит учащихся к самостоятельному открытию, чтобы учащиеся сами подошли к формулировке различия между позиционным и непозиционным принципом записи чисел.

К примеру, учитель, перед тем как начать излагать новую тему, например, с использованием презентации, объясняет ученикам, для чего нужна система счисления и как она возникла, а потом вводить понятие «система счисления». Учащимся предлагается проанализировать запись числа с использованием арабских цифр, и запись числа с использованием римских цифр.

В римском способе записи чисел значение цифры не зависит от ее позиции, а в арабском – зависит. И на основании указанного различия приводятся понятия «непозиционная» и «позиционная». После этого формулируется определения.

Далее учитель приводит примеры различные непозиционных систем счисления.

Для того чтоб учащиеся понимали различие понятие цифра и числа, наглядно рассматривается два числа 52 и 25. И говорится, что цифры одни и те же – 5 и 2, задаем такой вопрос «А чем же данные числа отличаются?», сделав ударение «позиция», говорим, позиция цифры в числе, то есть цифры поменяли местами.

Значение цифры не зависит от ее положения в числе. Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется. Делается вывод, что в непозиционных системах счисления выполнять вычисления неудобно, потому что запись больших чисел требует введения новых символов, невозможно представлять дробные и отрицательные числа, сложно выполнять простейшие арифметические операции.

Далее нужно дать понять учащимся, что позиционные системы счисления существует множество и отличаются они друг от друга алфавитом. Сказать, что произвольным основанием может быть любое основание позиционной системы счисления – это могут быть и пятеричная, троичная система счисления и т.д.

Следующий вопрос, изучаемый в этой теме – методы перевода чисел из одной системы счисления в другую.

Учитель объясняет на примерах алгоритм перевода чисел из десятичной системы счисления.

На рисунке 1 представлен пример перевода числа 20₁₀ в двоичную систему счисления, а полученные остатки записываются в обратном порядке, начиная с последнего частного:

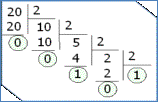
Рис.1. Перевод числа 20₁₀ в двоичную систему счисления.

Очень хорошо, когда на каждом примере, после объяснение, вызванный к интерактивной доске учителем ученик решает на доске, так у них развивается мотивация, соображение и остальным учащимся четко видно и возможно вместе разобраться в ошибке, если ученики не правильно решил.

Учитель рассказывает, что двоичные числа для восприятия человеком не очень удобны, так как их запись довольно длинная. Поэтому нужны системы счисления, которые позволили бы существенно сократить запись числа, и в них легко было бы перевести двоичные числа. С этой целью используются 8-ричная и 16-ричная система счисления, то есть системы с основанием 2³ и 2⁴ соответственно. Основание этих систем счисления позволяют каждую 8-ричную или 16-ричную цифру заменить тремя или четырьмя двоичными цифрами, и наоборот, три или четыре двоичные цифры можно: перевести цифру из одной системы счисления в другую через десятичную систему, воспользоваться таблицей соответствия натуральных чисел.

Решение примеров учитель с объяснением записывает на интерактивной доске, а учащиеся записывают данные в тетради. Преподавание темы «Системы счисления» проходят на уроке с использованием презентаций, демонстраций примеров, применением раздаточного материала для самостоятельной работы, таблицами.