Строительство и архитектура / 7. Водоснабжение и канализация

К.т.н. Калякин А.М., Чеснокова Е.В., Сауткина Т.Н., Толочкова И.С., Хурчакова А.А.

Саратовский государственный технический университет

имени Гагарина Ю.А., Россия

Особенности кинематики течения перед цилиндром при обтекании его открытым потоком

Часть 2

Оценка интенсивности нисходящих токов

Для получения аналитических оценок рассмотрим незатопленное обтекание прямого кругового цилиндра потоком реальной жидкости. Дно вначале предполагается плоским и не размываемым.

В [1, 2] показано, что в соответствии с опытными данными перед цилиндром картина линий тока в горизонтальных плоскостях, параллельных дну, близка к картине линий тока при потенциальном обтекании цилиндра (предполагаем, что самая нижняя такая плоскость отстоит от дна на расстоянии ).

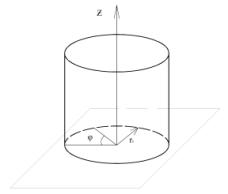
Рисунок 1.

В цилиндрической системе координат (вывод дан в [1, 2]) рис. 1, нами получены, после некоторых упрощений зависимости для скоростей

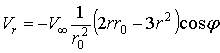(1)

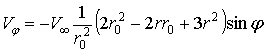, (2)

где – радиус цилиндра, – ширина кругового кольца, внутри которого наблюдаются нисходящие токи, – угол, отсчитываемый от оси набегающего потока, – скорость набегающего потока, изменяющаяся по глубине.

Вертикальную (вдоль оси ) составляющую находим из условия выполнения в каждой точке уравнения неразрывности

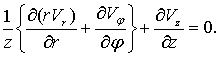(3)

Подставим (1) и (2) в (3) и для определения проинтегрируем полученное выражение от до H, где не равное нулю расстояние от дна.

Найдем в результате

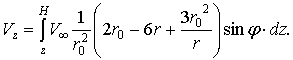(4)

Для возможно выбрать любой закон распределения скоростей по глубине (на бесконечности), но необходимо учитывать, что по мере приближения потока к поверхности цилиндра эпюра распределения скоростей будет искажаться, так что выбранный закон распределения будет выполняться лишь приближенно. В данном случае примем известный закон распределения скоростей при турбулентном режиме

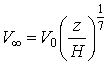(5)

где – расстояние от дна до рассматриваемой плоскости, – глубина потока, – одинаковая для всех горизонтальных сечений скорость подходящего потока.

Подставляя (5) в (4) и интегрируя, получим для составляющей

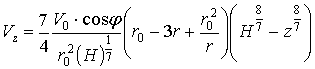. (6)

Компонента завихренности в цилиндрической системе будет иметь вид:

.

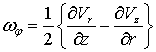Компонента представляет собой окружную скорость движения частиц в спиралевидных образованиях.

В нашем конкретном случае имеем

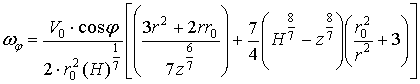(7)

Анализ формул (6) и (7) позволяет сделать следующие выводы:

1. Завихренность, т. е. величина по мере приближения к поверхности цилиндра возрастает; при возрастает до бесконечности. Эту особенность можно устранить, предположив, что (7) правильно отражает физику явления лишь до некоторого малого расстояния до цилиндра, при , меньшем физические свойства истечения иные.

2. Величина возрастает при стремлении к нулю и при одновременном стремлении и к нулю. Особенность увеличения до бесконечности при можно устранить, предложив, как и в предыдущем пункте, что уравнение (7) верно описывает особенности истечения лишь до некоторого расстояния от свободной поверхности. Это положение объясняет экспериментально отмеченный факт, что завихренность сконцентрирована вблизи поверхности цилиндра.

3. Величина принимает наименьшее значение при , т. е. на поверхности потока (при заданном распределении в виде (5)).

4. Справедливо следующее тождество [3]

(8)

( – вектор вихря).

Если вблизи некоторой поверхности происходит концентрация завихренности, то линия на этой поверхности параллельна (иначе не будет выполняться (8) [3]).

Составляющая направлена вдоль кривых, близких по форме к окружностям, а около окружности (вдоль образующих цилиндра) и образуются (как отмечалось при анализе экспериментальных данных) вихревые шнуры, что подтверждает основные этапы вывода (7) и согласуется с опытными данными.

На основе вышеизложенного можно предложить следующее предположение о физике явлений перед цилиндром при турбулентном режиме обтекания.

Завихренность потока возрастает по мере приближения его к поверхности цилиндра и концентрируется в тонком слое вблизи него; внутри этого слоя происходит перенос завихренности в форме движущихся вихревых шнуров подковообразной формы. Внутри каждой вихревой трубки линии тока напоминают спираль, рис. 3; каждая такая трубка подсасывает жидкость извне (в силу меньшего давления внутри вихря) и перемещает его вниз и вдоль своего направления.

При визуализации потока в его толще вихри у поверхности цилиндра видны по той причине, что краска концентрируется внутри них (вихрь обладает в данном случае свойством перемещать частицы жидкости к центру) и они становятся ясно видны на фоне потока.

В дальнейшем своем движении вихревой жгут (шнур), будучи устойчивым образованием, может деформироваться. Вихревые шнуры, доходя до дна, деформируются, двигаясь вдоль него; при растяжении их интенсивность увеличивается, они подсасывают твердые частицы и транспортируют их внутри себя за опору. Таким образом, генератором вихревых шнуров в потоке со сдвигом является боковая поверхность кругового цилиндра. После достижения ими нижней части цилиндра их можно рассматривать самостоятельно и, в частности, изучить динамику их взаимодействия с ямой размыва.

Шнуровые вихри (вихревые жгуты) не обязательно имеют большую скорость своего перемещения, но скорость их вращения весьма значительна. Вследствие этого эффект размыва складывается из большой скорости их вращения, эффекта подсасывания ими частиц и уноса их вдоль оси шнуров за цилиндр.

Таким образом, предположенная модель пригодна и для рассмотрения обтекания промежуточной мостовой опоры при размываемом дне.

В настоящее время распространено представление, что перенос массы у поверхности цилиндра ко дну существует в виде прямых нисходящих токов [4]. Такое представление, по нашему мнению, является упрощенным и не имеет, к настоящему времени, прямого подтверждения экспериментами.

Как следует из (6), скорость у самой поверхности цилиндра максимальна, что позволяет определить направление вращения внутри вихревых трубок.

Литература:

1. Калякин А.М. Метод решения уравнений Навье-Стокса для обтекания препятствий типа мостовой опоры (с использованием эвристических гипотез). Совершенствование методов гидравлических расчетов водопропускных и очистных сооружений: межвуз. науч. сб. Саратов: Сарат. гос. Техн. ун-т, 1996. С. 68-74.

2. Калякин А.М. Модель процесса размыва перед препятствием типа мостовой опоры на основе представлений о вихре. Совершенствование методов гидравлических расчетов водопропускных и очистных сооружений: межвуз. науч. сб. Саратов: Сарат. гос. Техн. ун-т, 1997. С. 33-43.

3. Лойцянский Л.Г. Механика жидкости и газа. М.: Дрофа, 2003. 840 с.

4. Журавлев М. М. Местный разрыв у опор мостов. М.: Транспорт, 1984. 112 с.