СТРОИТЕЛЬСТВО И АРХИТЕКТУРА: Водоснабжение и канализация

Куницкий С.О., аспирант кафедры водоснабжения и бурового дела

Национальный университет водного хозяйства и природопользования, Украина, Ривне

Математическая модель роста потерь напора в фильтрующей загрузке фильтра

Чрезвычайно актуальной проблемой в наше время является проблема очистки воды и ее снабжения потребителям. Важной составной частью экономики государства, экономического района или области, является водохозяйственный комплекс. Главное его задание – обеспечить в необходимом количестве социальных, гигиенических, культурно-эстетичных и других потребностей промышленности и населения Украины.

Большинство сельского населения Украины потребляют воду подземных горизонтов, которые залегают на глубине 50-150 м. Качество воды чаще всего не отвечает требованиям к питьевой воде, поскольку содержит в своем составе повышенную концентрацию железа (до 5 мг/дм³ и больше), сероводороду и свободной углекислоты. Поэтому в системе водоснабжения населенных пунктов следует предусматривать станции обезжелезивания воды [1].

При эксплуатации водоочистных объектов важное место занимает оптимизация режима процесса очистки воды, который достигается за счет математических моделей технологических процессов [2, 3].

Экспериментальные исследования процесса обезжелезивания воды проводились на лабораторной установке из использования модельного раствора. Как фильтрующий материал фильтра использовалась зернистая пинополистирольна зазрузка эквивалентным диаметром 2,8 мм

В качестве контролируемых параметров для моделирования процесса обезжелезивания воды использовались такие контролируемые параметры: входная концентрация железа С_вx, скорость фильтрования V_ф и длительность фильтроциклу Т_ф. В качестве неконтролированного исследуемого параметру - потери напора в фильтрующей загрузке при полной ее промывке Н.

Для выявления статистического взаимодействия [2, 3] вышеупомянутых факторов был проведен ряд фильтроциклив длительностью 8 часов с разной входной концентрацией железа в модельном растворе (1,0…2,0 мг/дм³). Исследование потерь напора проводилось в диапазоне скоростей фильтрования от 4 до 7 м/год. Показатель величины потерь напора Н снимался трижды во время каждого фильтроциклу.

Функциональная зависимость роста потерь напора в натуральном виде можна представить в виде:

(1)

Для прогнозирования изменения потерь напора в фильтрующей пинополистирольний загрузке при полной ее промывке была выведена математическая зависимость роста потерь напора (2):

Н = -0,79 + 1,36 С_вx + 1,1197V_ф + 0,2017Т_ф – 0,12С_вx Т_ф + 0,0385 V_фТ_ф (2)

Данное уравнение регрессии можно использовать для прогнозирования роста потерь напора со временем в пинополистирольний фильтрующей загрузке в диапазоне скоростей от 4 до 7 м/год и входной концентрации железа в воде от 1,0 до 2,0 мг/дм³.

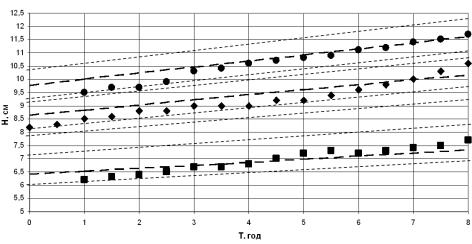
Рис. 1. График зависимости в фильтрующей загрузке, при ее полной промывке со входной концентрации железа 2,0 мг/дм³

В зависимости от типа загрузки, интенсивности промывки, объема промывной воды, длительности промывки, степень очистки загрузки может быть разной. В процессе эксплуатации водоочистительных фильтров достаточно часто придется наблюдать неполную промывку фильтрующей загрузки. Поэтому математическая зависимость, которая описывает изменение роста потерь напора в фильтрующей пинополистирольний загрузке при неполной ее промывке в течение определенного промежутка времени представленная формулой (3):

Н = 1,81 - 1,36 С_вx - 0,7V_ф - 0,14Т_ф + 0,26С_вx V_ф + 0,06 V_фТ_ф (3)

Зависимость (3) можно использовать для прогнозирования роста потерь напора со временем в пинополистирольний фильтрующей загрузке при неполной ее промывке в диапазоне скоростей от 5 до 7 м/год и входной концентрации железа до 2,0 мг/дм³.

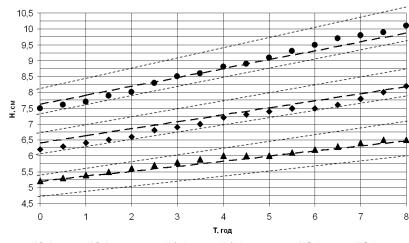
Рис. 1. График зависимости в фильтрующей загрузке, при ее неполной промывке со входной концентрации железа 2,0 мг/дм³

Литература:

1. Орлов В.О. Водоочисные фильтри из зернистою засипкою. Монография – Ривне: НУВГП, 2005. – 163 с. 2. Любарский Г.Я. и др. / Математическое моделирование и эксперимент.- Київ: Наукова думка, 1987. 3. Горский В.Г. Планирование промышленных экспериментов. / В.Г. Горский, Ю.П. Адлер – М.: Металургия, 1974, - 264 с.