К.т.н. Судариков А.Е.

Карагандинский государственный технический университет

Современные математические методы прогноза условий поддержания и крепления горных выработок

Горное производство – это, в первую очередь, обеспечение максимальной безопасности условий труда. Проявление давления горных пород на подземные выработки – причина многих катастроф и несчастных случаев в шахте. Горное давление относится к таким природным явлениям, которые требуют для своего управления обширных знаний в механике сплошных и сыпучих сред, расчете элементов систем отработки, специальных способов и средств натурных наблюдений, интерпретации наблюдений в пространстве и времени [1]. Здесь происходит как раз то, что мы называем искусством горного инженера который все это должен учесть и предвидеть.

Увеличение глубины разработки и усложнение горно-геологических и горнотехнических условий требуют более надежных методов прогнозирования горного давления как для разработки рациональных паспортов крепления горных выработок, так и для безопасного ведения добычных работ.

Увеличение применения в настоящее время анкерного крепления по сравнению с рамным креплением требует более точного прогноза в отношении геомеханических процессов происходящих вокруг горных выработок.

Существующие нормативные методики прогноза проявления горного давления не всегда могут отразить многообразие факторов оказывающее решающее влияние на его проявления.

Применяемые в настоящее время математические методы моделирования позволяют с большей точностью учитывать многообразие различных факторов оказывающее решающее значения на проявления горного давления вокруг выработок [2]. Однако в большинстве случаев данные методы требуют настройки или адаптации программы под конкретные условия горного предприятия что, в свою очередь, усложняет их применение.

Применение математических методов так же сдерживается из-за существенной неоднородности горного массива на его различных локальных участках.

Определение напряженно-деформированного состояния (НДС) приконтурного массива вокруг полости любой формы не представляет трудности в случае применения специализированных математических программ и современной компьютерной техники. Наибольшую сложность после определения НДС представляет нахождения зоны неупругих деформаций (ЗНД) или зоны разрушения вокруг полости определенной формы которая и определяет горное давление и, в конечном итоге, это служит основанием для разработки параметров крепления горной выработки. Трудность с определением главного фактора разрушения горной породы, не совпадения условий нагружения породы в массиве и при испытании образцов на прочность, масштабный эффект и природное изменение физико-механических свойств на разных участках исследуемого массива иногда сводят на нет сложные математические расчеты НДС массива.

Здесь мы приходим противоречию: можно провести точный расчет методами сопротивления материалов и строительной механики несущей способности крепи горной выработки только в случае знания величины и характера её нагружения. Из-за невозможности точного определения нагрузки на крепи при проявлении горного давления и характера нагружения нет возможности проведения точного инженерного расчета горных конструкций, что приводит или к неоправданному завышению коэффициента надежности таких конструкций и перерасходом материалов крепи или к их разрушению зачастую связанную с человеческими жертвами на производстве.

В данном случае в силу неопределенности и невозможности точного определения нагрузок решение такого типа задач не всегда должно начинаться с расчетов на прочность. Первоначально необходимость как то упорядочить и привести аналогию с использованием математических методов, а затем разрабатывать более конкретные инженерные решения.

Можно провести аналогию такого подхода использования в экономических системах. Турбулентность внешней среды современной мировой экономики не позволяет решать экономические задачи однозначно как инженерные. Здесь также на конечные экономические показатели оказывают влияние слишком большое число факторов. Еще в начале прошлого века математиками были разработаны методы (эконометрический анализ) помогающие отыскать наиболее существенное влияние на тот или иной экономический показатель [3]. Развитие информационных технологий позволило резко упростить многие сложные математические вычисления и применить достаточно сложный математический аппарат широкому кругу исследователей.

Использование корреляционно-регрессионного анализа, построение парных и множественных линейных моделей при исследовании геомеханических процессов встречается в большинстве диссертационных работ и научных исследований в горном деле. Использование этих методик всегда ограниченно конкретными условиями для которых проводились исследования. Хотя следует отметить, что данные методы позволяют в некоторых случаях использовать простые математические зависимости для моделирования сложных процессов в массиве.

Более сложным и трудоемким можно назвать процесс исследований применяющий более современные методы вычисления и более современное программные продукты. В этом случае на первом этапе проводится кластерный анализ условий расположения техногенных обнажений позволяющий разделить все многообразие существующих условий заложения горных выработок. А на втором и последующих этапах предлагается применение программ позволяющих обнаружить связь между природными факторами и параметрами крепления выработок (такая связь может быть найдена от самых простых корреляционных моделей корреляции до современных нейросетей). Такая методика позволит сначала уменьшить разброс факторов влияющих на устойчивость горных выработок в различных кластерах, а затем разработать и определить рациональные параметры крепления горных выработок в каждом кластере.

В отличие от задач классификации, кластерный анализ не требует априорных предположений о наборе данных, не накладывает ограничения на представление исследуемых объектов, позволяет анализировать показатели различных типов данных (интервальным данным, частотам, бинарным данным). При этом необходимо помнить, что переменные должны измеряться в сравнимых шкалах.

Кластерный анализ позволяет сокращать размерность данных, делать ее наглядной [4].

Задачи кластерного анализа можно объединить в следующие группы:

Разработка типологии или классификации.

Исследование полезных концептуальных схем группирования объектов.

Представление гипотез на основе исследования данных.

Проверка гипотез или исследований для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных.

Как правило, при практическом использовании кластерного анализа одновременно решается несколько из указанных задач.

Размер кластера может быть определен либо по радиусу кластера, либо по среднеквадратичному отклонению объектов для этого кластера. Объект относится к кластеру, если расстояние от объекта до центра кластера меньше радиуса кластера. Если это условие выполняется для двух и более кластеров, объект является спорным.

Неоднозначность данной задачи может быть устранена экспертом или аналитиком.

Работа кластерного анализа опирается на два предположения. Первое предположение - рассматриваемые признаки объекта в принципе допускают желательное разбиение пула (совокупности) объектов на кластеры. Второе предположение - правильность выбора масштаба или единиц измерения признаков.

Выбор масштаба в кластерном анализе имеет большое значение. Тогда, при расчете величины расстояния между точками, отражающими положение объектов в пространстве их свойств, переменная, имеющая большие значения будет практически полностью доминировать над переменной с малыми значениями. Таким образом из-за неоднородности единиц измерения признаков становится невозможно корректно рассчитать расстояния между точками. Эта проблема решается при помощи предварительной стандартизации переменных. Стандартизация (standardization) или нормирование (normalization) приводит значения всех преобразованных переменных к единому диапазону значений путем выражения через отношение этих значений к некой величине, отражающей определенные свойства конкретного признака. Наряду со стандартизацией переменных, существует вариант придания каждой из них определенного коэффициента важности, или веса, который бы отражал значимость соответствующей переменной.

Решением задачи кластерного анализа являются разбиения, удовлетворяющие некоторому критерию оптимальности. Этот критерий может представлять собой некоторый функционал, выражающий уровни желательности различных разбиений и группировок, который называют целевой функцией. Например, в качестве целевой функции может быть взята внутригрупповая сумма квадратов отклонения:

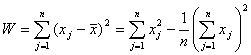
где x_j - представляет собой измерения j-го объекта.

Для решения  задачи кластерного анализа необходимо определить понятие сходства и разнородности.

Понятно то, что объекты i-ый и j-ый попадали бы в один кластер, когда расстояние (отдаленность) между точками Х_i и Х_j было бы достаточно маленьким и попадали бы в разные кластеры, когда это расстояние было бы достаточно большим. Таким образом, попадание в один или разные кластеры объектов определяется понятием расстояния между Х_i и Х_j из Е_р, где Е_р - р-мерное евклидово пространство.

Методы кластерного анализа можно разделить на две группы: иерархические; неиерархические. Рассмотрим иерархические методы кластерного анализа Суть иерархической кластеризации состоит в последовательном объединении меньших кластеров в большие или разделении больших кластеров на меньшие

Иерархические методы кластеризации различаются правилами построения кластеров. В качестве правил выступают критерии, которые используются при решении вопроса о "схожести" объектов при их объединении в группу (агломеративные методы) либо разделения на группы (дивизимные методы).

Иерархические агломеративные методы (Agglomerative Nesting, AGNES) Эта группа методов характеризуется последовательным объединением исходных элементов и соответствующим уменьшением числа кластеров. В начале работы алгоритма все объекты являются отдельными кластерами. На первом шаге наиболее похожие объекты объединяются в кластер. На последующих шагах объединение продолжается до тех пор, пока все объекты не будут составлять один кластер.

Иерархические дивизимные (делимые) методы (DIvisive ANAlysis, DIANA) Эти методы являются логической противоположностью агломеративным методам. В начале работы алгоритма все объекты принадлежат одному кластеру, который на последующих шагах делится на меньшие кластеры, в результате образуется последовательность расщепляющих групп.

Меры сходства. Для вычисления расстояния между объектами используются различные меры сходства (меры подобия), называемые также метриками или функциями расстояний. Квадрат евклидова рас стояния. Манхэттенское расстояние Процент несогласия.

Методы объединения или связи. Когда каждый объект представляет собой отдельный кластер, расстояния между этими объектами определяются выбранной мерой. Возникает следующий вопрос - как определить расстояния между кластерами? Существуют различные правила, называемые методами объединения или связи для двух кластеров. Метод ближнего соседа или одиночная связь. Метод наиболее удаленных соседей Метод Варда и т д.

Программная реализация алгоритмов кластерного анализа широко представлена в различных инструментах Data Mining, которые позволяют решать задачи достаточно большой размерности [6]. Например, агломеративные методы реализованы в пакете SPSS, дивизимные методы - в пакете Statgraf.

Вторым этапом исследований после решения задачи кластерного анализа должна быть программа позволяющая на каждом кластере исследовать геомеханические процессы. В этом случае мы приходим или к стандартным методам которые используются в настоящее время в горном деле (нормативные методики, численное моделирование, использование аналогии и т.д.) или к наиболее современному методу получившее в настоящее время большое распространение - нейронные сети (НС) [5].

Широкий круг задач, решаемый НС, не позволяет в настоящее время создавать универсальные, мощные сети, вынуждая разрабатывать специализированные НС, функционирующие по различным алгоритмам.

Несмотря на существенные различия, отдельные типы НС обладают несколькими общими чертами.

Во-первых, основу каждой НС составляют относительно простые, в большинстве случаев – однотипные, элементы (ячейки), имитирующие работу нейронов мозга. Далее под нейроном будет подразумеваться искусственный нейрон, то есть ячейка НС. Каждый нейрон характеризуется своим текущим состоянием по аналогии с нервными клетками головного мозга, которые могут быть возбуждены или заторможены. Он обладает группой синапсов – однонаправленных входных связей, соединенных с выходами других нейронов, а также имеет аксон – выходную связь данного нейрона, с которой сигнал (возбуждения или торможения) поступает на синапсы следующих нейронов. Возвращаясь к общим чертам, присущим всем НС, отметим, во-вторых, принцип параллельной обработки сигналов, который достигается путем объединения большого числа нейронов в так называемые слои и соединения определенным образом нейронов различных слоев.

Теоретически число слоев и число нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами компьютера или специализированной микросхемы, на которых обычно реализуется НС. Чем сложнее НС, тем масштабнее задачи, подвластные ей.

Выбор структуры НС осуществляется в соответствии с особенностями и сложностью задачи. Для решения некоторых отдельных типов задач уже существуют оптимальные, на сегодняшний день, конфигурации.

Очевидно, что процесс функционирования НС, то есть сущность действий, которые она способна выполнять, зависит от величин синаптических связей, поэтому, задавшись определенной структурой НС, отвечающей какой-либо задаче, разработчик сети должен найти оптимальные значения всех переменных весовых коэффициентов (некоторые синаптические связи могут быть постоянными).

Этот этап называется обучением НС, и от того, насколько качественно он будет выполнен, зависит способность сети решать поставленные перед ней проблемы во время эксплуатации. На этапе обучения кроме параметра качества подбора весов важную роль играет время обучения. Как правило, эти два параметра связаны обратной зависимостью и их приходится выбирать на основе компромисса.

Обучение НС может вестись с учителем или без него. В первом случае сети предъявляются значения как входных, так и желательных выходных сигналов, и она по некоторому внутреннему алгоритму подстраивает веса своих синаптических связей. Во втором случае выходы НС формируются самостоятельно, а веса изменяются по алгоритму, учитывающему только входные и производные от них сигналы.

Представленный алгоритм решение задач геомеханики с использованием современных численных методов и пакетов прикладных программ позволит более индивидуально подходить к вопросам горного давления при меняющихся условиях расположения техногенных обнажений в массиве и тем самым обеспечит разработку рациональных параметров крепления горных выработок

ЛИТЕРАТУРА

1. А.В. Гальянов, Журнал "Маркшейдерия и недропользование" № 1 - 2011г.

2. Судариков А.Е., Мусин Р.А. Численное моделирование геомеханических процессов и графические пакеты прикладных программ Труды Международной научно-практической конференции «Актуальные проблемы горно-металлургического комплекса Казахстана». – Караганда: Изд-во КарГТУ, 2005, С. 29-31

3. Судариков А.Е. Эконометрика (учебное пособие) ISBN 9965 – 02-017-5 Карагандинский университет Бизнеса, Ууправления и Права Караганда 2002.

4. Судариков А.Е., Леонов В.В. К вопросу о сегментации рынка на базе современных информационных технологий Карагандинский университет Бизнеса, Управления и Права Караганда 2004, №10 С. 93-96

5. Судариков А.Е. Нейросети – теория сложных систем в экономике Караганда: Изд-во КарГТУ, Труды университета. Республ. Сборник. 2008, №2 С.69-72

6. Нейронные сети. STATISTICA Neural Networks: Пер. С англ. – М.: Горячая линия – Телеком. 2000.