Shapovalov I.O., Ignatyev V.V., Kobersi I.S.
Southern Federal University, Russian Federation
Moving
objects with intelligent robot group
The problem of
synthesis algorithm of intelligent robot group functioning, which should move
the flat body, located on a hard surface (Fig. 1) is considered in the paper.
In this case the moving body is the control object, and the robot group forms
control actions in accordance with the purpose of management. It's necessary to
find algorithms of the robot group functioning as the self-organizing control
part of the system.
The body 
has shape of circle, mass 
, radius 
and moment of inertia 
. Its motion is described by the
system of equations:
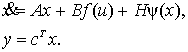(1)
Where 
is the state variable vector; 
is the control vector; 
is output variable vector; 
is the nonlinear vector-function, describing all actions of active
robots; 
is vector-function of perturbation actions; 
, 
, 
, 
are matrices and vector of known coefficients.
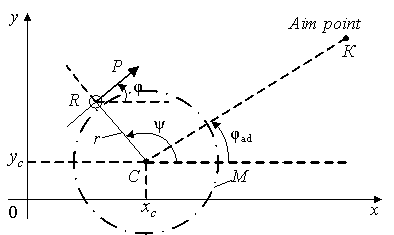
Fig. 1. The round body on flat surface
The 
-vector is consisted by next variables:
, 
are coordinates of the body gravity center; 
, 
are linear velocity projections on the coordinate axes; 
is the angle characterizing body orientation; 
is angular body velocity.
Intelligent robot group as control part of the system consists of n
identical autonomic transport robots considered in [1] in detail. Control
actions of each robot 
are described by vector
, where 
is pulling force of i-th robot, 
is angle characterizing direction of this force and
, 
. (2)
Because of the
constraints (2) there is only a certain number of possible values and
directions of the total pulling force in the system, which is proportional to
the number n of robots.
According to the
task robot group must form cluster by itself. The cluster is sub-group of
active robots solving the task of body moving along reference trajectory.
Motion conditions can change considerably on different trajectory parts.
Therefore task of robot group structure adaptation to current conditions
arises. From the control theory [2] point of view the system "robot
group-body" providing body 
motion along reference trajectory is distributed self-organizing
adaptive control system.
This control
system can be represented by block diagram on figure 2.
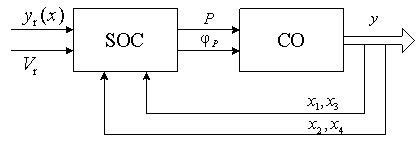
Fig. 2. Control
system block diagram
There are next
notations on fig. 2: SOC is the self-organizing controller; CO is the control object;
is reference trajectory; 
is reference object velocity. Group robots analyze current reference
trajectory area and corresponding real trajectory area on the basis of signals 
and effect on the control object with force 
directed at angle 
(fig. 2).
Schematically
group robot actions can be represented as it's shown on fig. 3.
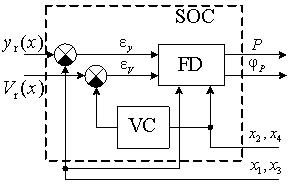
Fig.
3. Scheme of the self-organizing controller
According to fig.
3 measured body coordinates are used by group robots for future action calculation
and for calculation of current deviation 
real trajectory from reference trajectory 
.
The velocity
calculation block VC is designated for current body velocity 
calculation on the basis of the measured velocity projections on
the coordinate axes. Deviation 
of current velocity from reference velocity and deviation 
are used by forming device FD for control action forming. Control
actions 
and 
are determined from functional minimum condition:
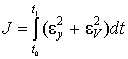, (3)
Where 
is time interval of object motion along trajectory.
The algorithm of intelligent robot
group functioning is created with using of collective interaction and pack
control principles which is proposed in [3].
Literature:
1.
Гайдук А.Р., Капустян С.Г., Шаповалов И.О. Оптимальное перемещение тела интеллектуальным
роботом // Мехатроника, автоматизация, управление. №7, 2009. С. 43-46.
2.
Александров А.Г. Оптимальные и адаптивные системы: Учеб. пособие для ВУЗов. М.:
Высшая школа, 1989.
3. Каляев И.А., Гайдук А.Р., Капустян С.Г.
Модели и алгоритмы коллективного управления в группах роботов. – М.: ФИЗМАТЛИТ,
2009.