Технические науки/12. Автоматизированные системы управления на производстве.

Чумаченко С.В.

Костанайский государственный университет им. А. Байтурсынова, Казахстан

Некоторые случаи определения нахождения САУ на границе устойчивости

Основной задачей автоматического управления является определение работоспособности систем автоматического управления (САУ), которая в свою очередь связана с понятием устойчивости.

Существует два способа определения устойчивости: экспериментальный и аналитический. Однако экспериментальный способ требует наличия готовой системы, т.е. таким способом можно определять устойчивость систем после модернизации или ремонта. При проектировании САУ используются аналитические способы определения устойчивости: алгебраические и частотные.

При определении устойчивости по расположению корней характеристического управления свободное движение системы описывается однородным дифференциальным уравнением: . (1)

Вынужденная составляющая выходной величины, зависящая от вида внешнего воздействия на устойчивость системы не влияет.

Решение уравнения (1) равно сумме: (2)

где C_k – постоянные, зависящие от начальных условий; p_k – корни характеристического уравнения .

Мнимая ось является границей устойчивости в плоскости корней. Если хотя бы один корень является «правым», то система будет неустойчивой. Если есть пара чисто мнимых корней, а все остальные корни «левые», то система находится на колебательной границе устойчивости. Если есть нулевой корень, то система находится на апериодической границе устойчивости. Если таких корней два, то система неустойчива [1]. Следовательно, системы у которых в характеристическом уравнении можно вынести за скобку р² являются неустойчивыми.

Если характеристическое уравнение системы имеет порядок выше третьего, то найти его корни затруднительно, т.к. отсутствуют формулы выражения корней через коэффициенты уравнений. Критерии Гурвица и Михайлова не позволяют определить количество «правых» корней характеристического уравнения. Критерий Рауса является достаточно простым способом определения устойчивости САУ высоких порядков, используя достаточно простой алгоритм. Однако при помощи данного критерия затруднительно определить нахождение системы на границе устойчивости: апериодической и колебательной.

Рассмотрим некоторые частные случаи определения нахождения САУ на границе устойчивости (по критерию Рауса с использованием других критериев устойчивости).

1). По критерию Гурвица система находится на апериодической границе устойчивости, если а_п = 0. Как будет выглядеть таблица Рауса в этом случае? Рассмотрим уравнения для систем 3 и 4 порядка.

Для системы с характеристическим уравнением: :

а0	а2	0
а1	0	0
а2	0	0
0	0	0

Для системы с характеристическим уравнением: :

а0	а2	0
а1	а3	0
	0	0
а3	0	0
0	0	0

Сравнив полученные таблицы для двух частных случаев, можно сделать вывод: аналогичная картина будет и при более высоких степенях характеристического уравнения, следовательно, если в последней строке таблицы Рауса все коэффициенты нулевые, то такая система находится на апериодической границе устойчивости [2].

Для рассмотрения нахождения САУ на колебательной границе устойчивости по критерию Рауса рассмотрим следующий частный случай: характеристическое уравнение системы имеет вид: . Корни данного уравнения: 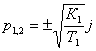, , . Для заполнения таблицы Рауса преобразуем заданное характеристическое уравнение и получаем: . По данному выражению заполним таблицу.

			0
		0	0
		0	0
0	0	0	0
?	?	?	?

При нахождении коэффициентов 5-ой строки таблицы, при определении строчного коэффициента получаем деление на нуль ().

Отсюда можно сделать вывод: если в строке с номером n (в нашем случае n=4) появляются нули, то такая система находится на колебательной границе устойчивости [2].

Литература:

1. Сенигов П.Н. Теория автоматического управления: Конспект лекций. - Челябинск: ЮУрГУ, 2001

2. Теория автоматического управления: учеб. пособие / М.М. Савин, В.С. Елсуков, О.Н. Пятина; под. ред. д.т.н., проф. В.И. Лачина. - Ростов н/Д: Феникс, 2007