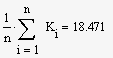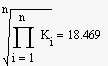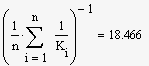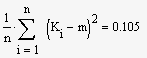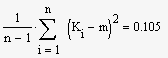Доповідь/Технічні науки – Автоматизовані системи управління на виробництві

УДК 681.513.68:622.24

Головата Ю.Б., Семенцов Г.Н., Скоробогата Н.З.

Івано-Франківський національний технічний університет нафти і газу

СТАТИСТИЧНІ ВЛАСТИВОСІ ФЛУКТУАЦІЙ ТИСКУ БУРОВОГО РОЗЧИНУ В ПРОЦЕСІ БУРІННЯ НАФТОВИХ І ГАЗОВИХ СВЕРДЛОВИН

Аналіз статистичних властивостей флуктуацій тиску бурового розчину в процесі буріння нафтових і газових свердловин є актуальною науково-практичною задачею у зв’язку з інтенсивним впровадженням в даний час оптимальних технологічних програм буріння та гідравлічних програм буріння для впроваджень доліт нового покоління в тому числі для доліт типу РДС. Раціональна гідравлічна програма для доліт РДС сприяє підвищенню механічної швидкості проходки і стійкості долота на вибої не менше ніж на 50%[1].

Проте, аналіз літературних джерел [наприклад, 1,2,3,4,7,11 та ін.] свідчить, що питання розробки і впровадження гідравлічних програм для буріння сучасними долотами недостатньо дослідженні. Це викликано тим, що процес буріння є складною динамічною системою з нечітко відомими математичними моделями, що функціонує за умов апріорі невідомих збурень щодо параметрів і структури об’єкта. Ідентифікація параметрів об’єкта ускладнюється невимірюваністю багатьох параметрів і показників процесу безпосередньо на вибої свердловини. Одним із вимірюваних параметрів є тиск бурового розчину, що подається в свердловину. На стадії дослідження об’єкта керування і експлуатації автоматизованої системи керування режимами буріння необхідні оцінки статистичних характеристик різних параметрів в задачах контролю для вибору тестових сигналів, планування експериментів, оцінки точності характеристик об’єкта керування, для вибору кроку дискретизації, діагностики стану обладнання та ін. В задачах автоматизованого керування вони потрібні також для вибору схем і аналізу якості регулювання, розрахунку параметрів налаштування регуляторів, синтезу оптимальних алгоритмів та ін.

Тому метою даної роботи є аналіз статистичних характеристик флуктуацій тиску бурового розчину в процесі буріння нафтових і газових свердловин.

Експериментальні дані для аналізу статистичних властивостей флуктуацій тиску бурового розчину були отримані на свердловині №15 «Делятин». Буріння здійснювалося роторним способом долотом типу 1АU269,9 СТГ на глибині 3198-3206 м з осьовою силою на долото F=220кН, швидкістю обертання долота n=1,33 , витратою бурового розчину м³/с [7].

Вихідні дані у вигляді дискретних значень через інтервал часу 1,5с були відтворені як графік залежності K(t) в програмному середовищі MATLAB[9] (рис.1).

Рисунок 1 – Відтворений графік флуктуацій тиску бурового розчину K(t).

Визначаємо математичне сподівання, дисперсію, квадратичне відхилення за допомогою програми Mathcad [10]:

Характеристика вибірки даних

Вектор спостережень

середнє геометричне

середнє гармонічне

дисперсія

зміщена оцінка

незміщена оцінка

cереднє арифметичне

середнє квадратичне відхилення

зміщена оцінка

незміщена оцінка

медіана

мода

Ексцесс

асиметрія

Визначаємо закон розподілу та перевіряємо його за допомогою критерію Пірсона. Для цього поділимо нашу вибірку значень х на інтервали та визначимо їх частоти. Об’єм вибірки складає: n=231. Впорядкуємо досліджувану вибірку у порядку зростання та поділяємо її на групи. В результаті розрахунків отримаємо наступні значення, що відображені в таблиці 1.

Таблиця 1

Результати групування вибірки даних

Номер інтервалу	Середина інтервалу	Частоти
1	17.8	1
2	17.9	2
3	18	7
4	18.15	14
5	18.25	22
6	18.3	30
7	18.4	34
8	18.5	42
9	18.75	33
10	18.8	19
11	18.9	11
12	19	8
13	19.1	6
14	19.25	3
15	19.5	1

За отриманими даними побудуємо полігон в програмному середовищі MATLAB[9]. Він приведений на рисунку 2.

Рисунок 2 – Полігон для визначення закону розподілу по даній вибірці

В середовищі MATLAB[9] побудуємо інтегральну функцію розподілу. Вона показана на рисунку 3.

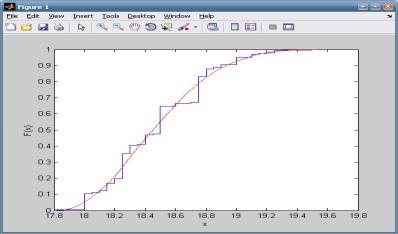
Рисунок 3 – Інтегральна функція розподілу

Для визначення закону розподілу скористаємося програмним середовищем Curve Expert[12]. В результаті отримаємо наступні варіанти, що зображені на рисунку 4:

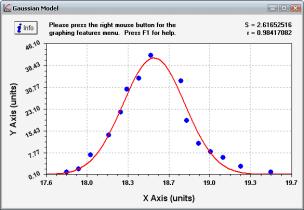
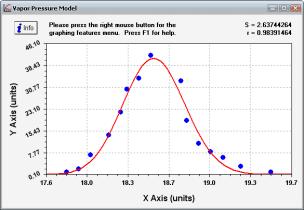
а) б)

Рисунок 4 – Визначення закону розподілу

У даному випадку найдоцільнішим є нормальний (Гауса) закон розподілу(рис.4а). Перевірки даної гіпотези за критерієм Пірсона та програмного середовища Mathcad[10] підтвердила справедливість цієї гіпотези. Визначаємо автокореляційну функції RКК(τ)(графік і рівняння).

Для визначення автокореляційної функції RКК(τ) скористаємося програмним середовищем (Partial) Autocorrelation Function - Free Statistics Software (Calculator) (рис.5).

Рисунок 5 – Графік автокореляційної функції

Для визначення рівняння автокореляційної функції скористаємося програмним середовищем Curve Expert. Виходячи з отриманих результатів найкраще графік описує експоненціально-косинусне рівняння, оскільки S – найменше значення, а r – найбільше. (рис.6):

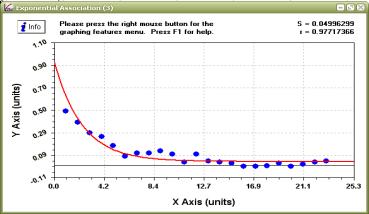
Рисунок 6 – Графік автокореляційної функції для визначення рівняння

Визначаємо спектральну густину досліджуваного процесу і будуємо графік.

Даній кореляційній функції відповідає спектральна густина:

(1)

Спектральна густина є додатною функцією у всьому діапазоні частот від 0 до ¥. Вона не містить відомостей про фази окремих гармонійних складових. За допомогою приведеної формули можна визначити спектральну густину по заданій аналітично автокореляційній функції Rкк(t)[5,6].

Визначимо спектральну густину, використовуючи пакет Mathcad. Попередньо ми визначили автокореляційну функцію Rкк(t) і застосувавши перетворення отримали:

Графік спектральної густини має такий вигляд (рис.7):

Рисунок 7- Графік спектральної густини

Тепер визначаємо АФХ формуючого фільтру

Спектральна густина (2) також може бути розкладена на два множники:

(3)

Отже, частотна передавальна функція фільтра, формуючого сигнал з прихованою періодичністю визначається:

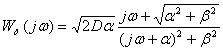(4)

Для нашого випадку частотна функція матиме вигляд:

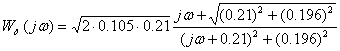(5)

Для побудови АФХ формуючого фільтра скористаємося програмним середовищем MATLAB (рис.8).

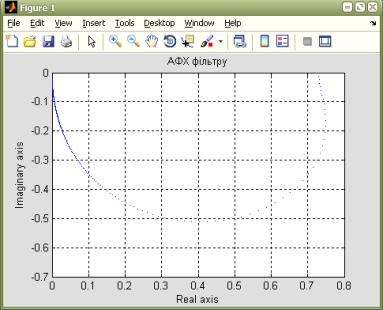
Рисунок 9 –АФХ формуючого фільтру

Висновки

Проведений аналіз статистичних властивостей флуктуацій тиску бурового розчину в технологічному процесі буріння нафтових і газових свердловин довів, що цей процес є стаціонарним ергодичним випадковим процесом з нормальним законом розподілу та експоненціально-косинусною автокореляційною функцією. Це дозволило визначити спектральну густину сигналу і амплітудно-фазову функцію формуючого фільтру. Отримані результати дають змогу обґрунтовано визначати в задачі автоматичного контролю тиску бурового розчину крок дискретизації цього параметру, а також структуру давача для системи автоматизованого керування режимами буріння.

Література:

1. Абдуялин Р.А. Пути повышения скорости бурения за рубежом / Р.А. Абдуялин, А.А. Шашин, Н.Н. Трубецкой . - М.: ВНИИОЭНТ, 1987. – 42с.

2. Закиров Н.Н. Влияния технологических параметров бурения скважин на механическую скорость и проходку на долото / Н.Н. Закиров // Бурение и нефть – 2003. - №6. – С.16-18.

3. Фадеєва О.В. Удосконалення математичної моделі технологічного процесу буріння нафтових і газових свердловин / О.В. Фадеєва // Вісник Хмельницького національного університету. Технічні науки. – 2008. - №6(123). – С.55-60.

4. Гутак О.В. Аналіз зв’язків показників ефективності процесу буріння на засадах системного підходу / О.В. Гутек, Г.Н. Семенцов // Нафтогазова енергетика – 2009.- №2(11).- С.94-99.

5. Семенцов Г.Н. Теорія автоматичного керування: [навч.посібн.] / Г.Н.Семенцов. – Івано-Франківськ: Факел. – 1999. –611с.

6. Лукас В.А. Теорія автоматического управления: [навч.посібн.] / В.А.Лукас – М.: Недра. – 1990. – 416с.

7. Семенцов Г.Н. Автоматизація процесу буріння свердловин / Г.Н.Семенцов. – Івано-Франківськ: Факел. – 1999. – 200с.

8. Семенцов Г.Н. Основи автоматизації виробничих процесів в бурінні:[навч/посібник] /Г.Н.Семенцов, Я.Р.Когуч, М.М.Дранчук,та ін.. – Івано-Франківськ: Факел. – 2004. – 269 с.

9. Мироновский Л.А. Введение в MATLAB: [навч/ посібник] / Л.А.Мироновский, К.Ю.Петрова. – СПб: ГУАП, -2006. - 164 с.

10. Васильєва О.А. Чисельні методи розв’язку задач у MathCad: [навч/посібник] / О.А.Васильєва, О.А.Гончаров, В.А.Коновалов, Н.А.Соловйова. - Краматорськ:ДДМА,- 2006.-108с.

11. Ред. В. С. Білецький Гірничий енциклопедичний словник: 3 т. /— Донецьк: Східний видавничий дім. - 2001—2004.

12. Програмні продукти Curve Expert, Free Statistics. – Режим доступу:http://en.freestatistics.info/stat.php