Доповідь/Технічні науки – Автоматизовані системи управління на виробництві

 

УДК 681.513.68:622.24

Семенцова А.О., Плитус А.В., Копистинський Л.О.,  Гутак О.В.,  

Івано-Франківський національний технічний університет нафти і газу

РЕЗУЛЬТАТИ АНАЛІЗУ СТАТИСТИЧНИХ ХАРАКТЕРИСТИК МОМЕНТУ НА ДОЛОТІ ПРИ БУРІННІ СВЕРДЛОВИН ЕЛЕКТРОБУРАМИ

Момент на долоті є одним із головних чинників, які визначають ефективність процесу буріння, як об’єкта керування. Для створення технічних засобів контролю моменту на долоті потрібна інформація про його статистичні характеристики. Проте аналіз літературних джерел [1, 2, 4, 5 та ін. ] показує недостатній об’єм проведених досліджень в напрямку створення алгоритмів функціонування пристроїв для контролю моменту на долоті, придатних для вирішення задач автоматизації процесу буріння. Тому метою даної роботи є розроблення алгоритму функціонування пристрою для одержання сигналу, пропорційного моменту на долоті, шляхом оброблення потоку енергії, яка потрапляє з електричної мережі до двигуна електробура.

Ефективність буріння нафтових і газових свердловин електробурами залежить від керувальних дій (осьової сили на долото і частоти його обертання), конструкції долота і потужності, яка доводиться до вибою свердловини. Потужність N1(t), яка споживається електробуром від мережі, перетворюється в потужність на валі Nв(t) зі значними втратами, тобто [1, 2]:

                                       ,                                              (1)  

де , 

 - втрати потужності в обмотці статора електродвигуна,

 - втрати потужності в сталі електродвигуна, викликані гістерезисом і вихровими струмами,

 - втрати потужності в обмотці ротора електродвигуна,

 - додаткові втрати потужності в електродвигуні,

 - втрати потужності на тертя в підшипниках, шпинделі та ін.,    

 - втрати потужності в струмопідвідному кабелі.

Підставляючи значення  із (1) в рівняння потужності на валі двигуна [1]:

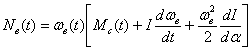                  ,                                       (2)

де   - кутова швидкість валу електродвигуна,

 - момент статичного опору на долоті,

 - сумарний момент інерції долота, приведений до валу електродвигуна,

-  кут повороту валу двигуна,

отримаємо вираз для моменту на валі двигуна електробура, тобто на долоті

                                                        (3)

     Вираз (3) запропоновано використовувати як алгоритм функціонування пристрою для одержання сигналу, пропорційного моменту на долоті, шляхом оброблення потоку енергії, яка поступає з електричної мережі до двигуна електробура.

Тоді відносна похибка вимірювання моменту на валі двигуна електробура дорівнює

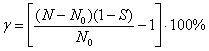               ,                                    (4)

де   - потужність, що споживається двигуном,

 - потужність, виміряна при холостому ході двигуна,

 - втрати потужності у струмопідвідному кабелі при холостому ході двигуна,

 - потужність, що споживається двигуном при відсутності осьової сили на долото,

 - ковзання двигуна.

За допомогою запропонованого пристрою вимірювання моменту отримано графік зміни моменту на долоті під час буріння свердловини №803Д електробуром Е170-8 №774 долотом 2К190ТЗ №337 в інтервалі 1858-1863 м в однорідних піщаниках верхньомінілітової підсвіти з остійною осьовою силою на долото 85 кН.

Флуктуації моменту на долоті являють собою випадкові процеси, механізм формування яких визначається великою кількістю факторів, наприклад, конструкцією низу бурильної колони, властивостями промивної рідини, твердістю породи, коливаннями напруги живлення в мережі електропостачання та іншими факторами (рис.1).

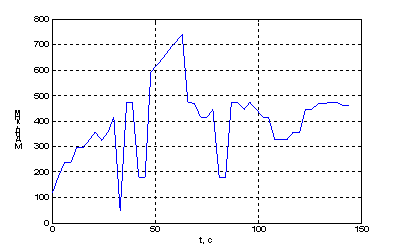
Рисунок 1 - Графік зміни моменту на долоті, отриманий в результаті обробки експериментальних даних у програмі MathLab

Для знаходження оцінок математичного сподівання, дисперсії та середньоквадратичного відхилення досліджуваного параметру скористалися програмою MathCad.

М а т е м а т и ч н е  с п о д і в а н н я

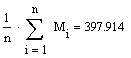
                              (5)

Д и с п е р с і я

з м і щ е н а  о ц і н к а

                                                                     

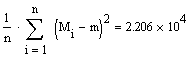
н е з м і щ е н а  о ц і н к а

 


                                                                                   

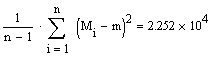
С е р е д н ь о к в а д р а т и ч н е  в і д х и л е н н я

 

з м і щ е н а  о ц і н к а          

               

н е з м і щ е н а  о ц і н к а          

                                      

Ці характеристики для кожного конкретного моменту є середніми з множини й визначаються одномірним законом розподілу.

Для визначення закону розподілу і перевірки його за допомогою критерію Пірсона скористалися програмою MathCad.

Згрупувавши експериментальні дані (kelk) (табл.1) та знайшовши їхні ймовірності появи (kpelk), побудували графік розподілу (рис.2).

Таблиця 1

Згруповані експериментальні дані

Згрупована вибірка

Кількість появи

118,3

1

177,8

5

237

2

296

2

325

1

325,9

4

335

1

355,6

4

414,8

5

444,5

5

462

1

462,8

1

468,4

3

474,1

8

592,6

1

622,2

1

651

1

681,5

1

711,1

1

740,8

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

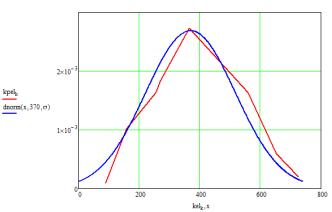
Рисунок 2 – Гістограма і закон розподілу для моменту на долоті

 

Припустили, що експериментальні дані підпорядковуються нормальному закону розподілу та перевірили вірність цьому закону розподілу за критерієм Пірсона χ2:

          к р и т е р і й  П і р с о н а                                                                           

                         

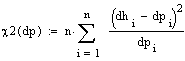
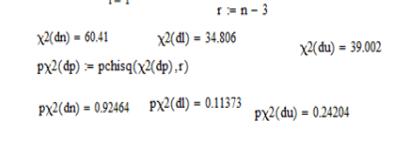
Для визначення автокореляційної функції використали програму MathСad. Для цього записали код програми, де вказано час, відповідні експериментальні дані і функція Rxx, яка визначає автокореляцію.

 

 

 

 

 

 

 

 

 

 

 

Отримали наступний графік нормованої автокореляційної функції  (рис.3):

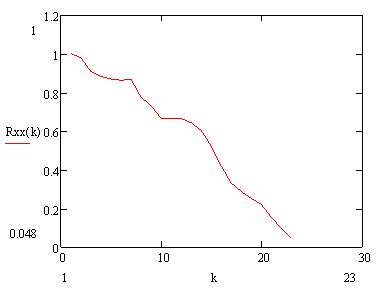
Рисунок 3 – Графік нормованої автокореляційної функції  для величини моменту на долоті

 

Графік автокореляційної функції підтверджує, що досліджуваний стохастичний процес М(t) є стаціонарним і ергодичним.

Відтворили автокореляційну функцію в програмі Curve Expert для підтвердження, що дана функція є найкращою для нашого випадку і для знаходження передавальної функцій.

Проаналізувавши три рівняння, вибираємо експоненціаль не рівняння:

                                  ,                                                   (6)                  

де а=1,065; b=-4.781.

Побудуємо графіки функцій, що описуються даним рівнянням (рис. 4). Як бачимо, графік повністю відтворює вище наведену автокореляційну функцію з коефіцієнтом кореляції r=0,996.

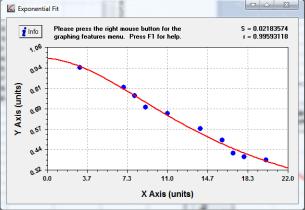
Рисунок 4 – Графік нормованої автокореляційної функції для моменту на долоті

 

Відзначимо, що при статистичному аналізі стаціонарних випадкових функцій зручно користуватись спектральною густиною випадкової функції. Спектральна густина є додатною функцією у всьому діапазоні частот від 0 до ¥. Вона не містить відомостей про фази окремих гармонійних складових. За допомогою приведеної формули можна визначити спектральну густину за заданою аналітично автокореляційною функцією.

Застосовуючи до кореляційної функції R(t)=De-α(τ) перетворення, визначили спектральну густину за формулою [3]:

                                           ,                        (7)

де D=1,0656933, α= -4.7819.

Підставивши наші дані в це рівняння отримали:

                                                                                          (8)

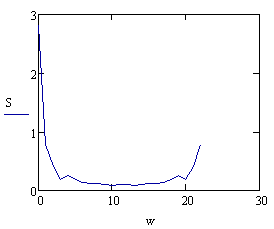
За отриманими даними побудували залежність S від w, використовуючи програму MathCad.

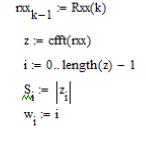
Для рівняння (8) графік спектральної густини зображений на рис. 5.

 

 

 

 

 

 

 

 

Рисунок 5 – Графік спектральної густини для моменту на долоті

Отримані результати дають змогу визначити властивості формуюючого фільтра.

Дійсно, частотна передавальна функція Wф(jω) фільтра зв’язана з спектральною густиною S(w) формуючого сигналу наступним співвідношенням [3]:

                                                       {Wф(jω)}2=S(w).                                        (9)

Для пошуку функції Wф(jω) необхідно розкласти спектральну густину S(w) на спряжені множники Wф(jω) і Wф(-jω). З цих двох множників фізично реалізуємо  у вигляді фільтра лише перший множник, в якому нулі і полюси (корені чисельника і знаменника) знаходяться у верхній півплощині.

Для сигналу з експоненціальною кореляційною функцією (6) маємо [3]:

                                                                             (10)

Звідси частотна функція фізично реалізованого фільтра:

                                                                                                 (11)

Виведемо графіки для АФХ формуючого фільтру за допомогою програми MathСad.

 

 

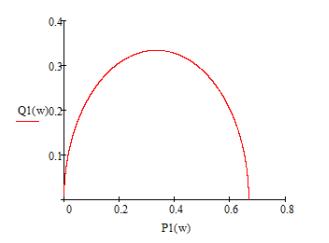
Рисунок 6 – Графік АФХ формуючого фільтра для вимірювання величини моменту на долоті

 

Висновок

Аналіз статистичних характеристик моменту на долоті при бурінні свердловини електробуром Е170-8 довів, що досліджуваний параметр підпорядковується нормальному закону розподілу та має експоненціальну автокореляційну функцію, що дозволило визначити спектральну густину  досліджуваного параметру і амплітудно-фазову характеристику формуючого фільтру.    

Література

1. Семенцов Г. Н. Автоматизація процесу буріння свердловин / Г. Н. Семенцов // Івано-Франківськ,:Факел –1997 – 300 с.

2. Фоменко Ф. Н. Бурение скважин электробуром / Ф. Н. Фоменко// М.: Недра – 1974. – 272 с.

3. Семенцов Г. Н. Теорія автоматичного керування: [навчальний посібник] / Г. Н. Семенцов // Івано-Франківськ: ІФНТУНГ – 1999 – 611 с.

4. Гутяк О. В. Ідентифікація і контроль координатних збурень у процесі поглиблення нафтових і газових свердловин / О. В. Гутяк, Н. В. Сабат, А. І. Лагойда // Нафтогазова енергетика – 2011. - №2(15). – с.78-84.

5. Семенцова А. О. Аналіз методів і засобів автоматизованого контролю енергетичних показників занурного електроприводу, що використовується при бурінні свердловин / А. О. Семенцова, О. В. Фадєєва // академічний вісник – 2004. – №13. – с.108-109

 

 

 

 

 

*