Каряченко
Н.В.
Национальная металлургическая академия
Украины
дифференциальноЕ уравнениЕ поперечных
колебаний канатов ГРУЗОТРАНСПОРТИРУЮЩИХ
УСТРОЙСТВ С ПОДВИЖНОЙ ИНЕРЦИАЛЬНОЙ
НАГРУЗКОЙ в общем виде
Поперечные колебания канатов имеют большое влияние
на динамику грузотранспортирующих канатных устройств, несущих подвижную
инерциальную нагрузку. Поэтому, исследование поперечных колебаний
канатов таких устройств является важной и актуальной задачей, без
решения которой невозможно правильно качественно и количественно
оценить динамические процессы, происходящие в этих системах.
Задача об изучении поперечных колебаний канатов
с подвижной распределенной и сосредоточенной инерциальной нагрузкой
сводится к решению линейных дифференциальных уравнений гиперболического
типа со смешанной производной. Применение классической схемы разделения
переменных в действительной области искомых функций к решению таких
уравнений невозможно. Разделение переменных неклассическим способом
[1-3],
в основу которого положен выбор решения в виде специального двухчленного
представления, приводит к приближенным, а в ряде задач точным, решениям этих уравнений.
Рассмотрим малые поперечные колебания каната одной
из ветвей грузотранспортирующей канатной установки, состоящей
из двух шкивов с натянутым на них упругим канатом, движущимся с постоянной
скоростью с прикрепленными к нему на равных расстояниях сосредоточенными
грузами. Канат моделируем гибкой нитью, отражающей его физические
свойства. Для
учета масс сосредоточенных грузов в выражении погонной массы каната
используем дельта-функцию Дирака d(x). Опираясь на общую постановку задачи, после необходимых
преобразований, пренебрегая бесконечно малыми более высокого
порядка малости, после перехода к неподвижной системе координат дифференциальное
уравнение одной из ветвей каната примет вид
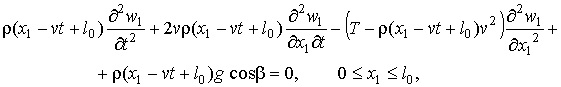 (1)
(1)
где ![]() - погонная масса
каната и прикрепленных к нему грузов в неподвижной системе координат, при
постоянной скорости движения v
подвижной системы координат, связанной с канатом, и постоянной во времени геометрической
области изменения координаты
- погонная масса
каната и прикрепленных к нему грузов в неподвижной системе координат, при
постоянной скорости движения v
подвижной системы координат, связанной с канатом, и постоянной во времени геометрической
области изменения координаты ![]() ;
;
![]() - расстояние между
центрами шкивов;
- расстояние между
центрами шкивов; ![]() - поперечное отклонение
одной из ветвей каната; Т - натяжение каната.
- поперечное отклонение
одной из ветвей каната; Т - натяжение каната.
Переходя в
уравнении (1) к безразмерным координатам и времени
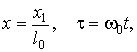
а
также учитывая
малую скорость движения, т.е. малое изменение положения элемента
вдоль оси за период колебаний, и вводя малый безразмерный параметр
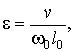
дифференциальное
уравнение поперечных колебаний каната примет вид:
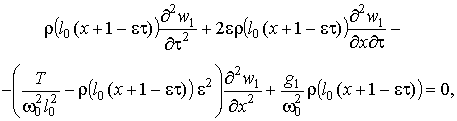 (2)
(2)
с границами изменения ![]() .
.
В уравнении (2) ![]() - частота колебаний
однородного каната закрепленного по концам, равная
- частота колебаний
однородного каната закрепленного по концам, равная 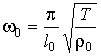 ,
, ![]() .
.
Дифференциальное
уравнение (2) необходимо решить при следующих граничных и начальных
условиях
![]() (3)
(3)
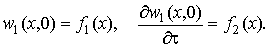 (4)
(4)
В (2) выражение et, учитывая его малость,
так как время движения ограничено, будем рассматривать как параметр, а также
будем пренебрегать в этом уравнении членом, имеющим множителем e2.
Если
на канате постоянной погонной массы имеются сосредоточенные грузы,
то выражение для r
можно преобразовать к следующему виду, следуя [4]
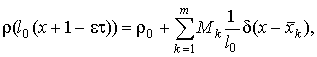
где
![]() ,
, ![]() - погонная масса каната,
- погонная масса каната, ![]() - масса груза,
сосредоточенного в точке
- масса груза,
сосредоточенного в точке ![]() .
.
Решение неоднородного
уравнения (2), состоит из суммы общего решения однородного уравнения
w(x,t) и частного решения
неоднородного уравнения w0(x)
![]()
где w(x,t)- удовлетворяет однородному уравнению,
соответствующему (2), w0(x)
- удовлетворяет уравнению (6), записанному
с учетом выражения для r.
Учитывая
вид граничных условий для w1(x,t) (3), можно утверждать,
что если w(x,t) и w0(x) будут удовлетворять (3), то и сумма их, равная
w1(x,t), будет удовлетворять
этим граничным условиям.
Построим частное решение неоднородного дифференциального
уравнения, соответствующего (2). С учетом выражения для r, запишем уравнение,
удовлетворяющее w0(x)
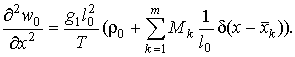 (5)
(5)
Используя преобразование Лапласа [5] перейдем в
(5) к изображению функции w0(x),
учитывая, что w0(0) = 0
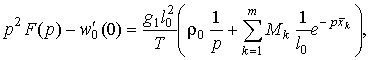
откуда ![]() запишется в виде
запишется в виде
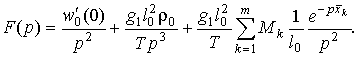
Переходя обратно от
изображения F(p) к оригиналу, получим
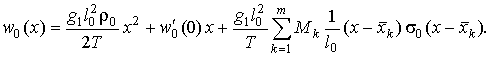 (6)
(6)
Из второго граничного
условия ![]() определим
определим ![]()
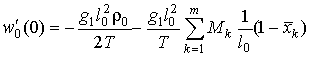 .
.
Окончательно, запишем
частное решение неоднородного уравнения, соответствующее уравнению
(2)
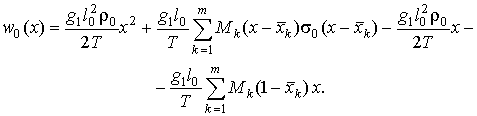
Литература.
1.
Горошко О.А. Собственные и “сопровождающие” колебания в системах
с подвижными инерционными нагрузками // Тр.5-й Междунар.
конф. по нелинейным колебаниям. -
Т.3. - 1970. - С. 215-220.
2.
Горошко О.А., Савин Г.Н. Введение в механику деформируемых одномерных
тел переменной длины. -
К., 1971. -
224 с.
3.
Горошко О.А., Демьяненко А.Г., Киба С.П. Двохвильові процеси в механічних
системах. -
К., 1991. -
188 с.
4.
Гельфанд И.М., Шилов Г.Е. Обобщенные функции и действия над ними. - М.: Физматгиз,
1958.
5.
Дёч Г. Руководство к практическому применению преобразования Лапласа
и Z-преобразования.
- М., 1971. - 288 с.