Чу Ким Хунг, Буй Тхань Хай, Чан Ван Дык

Донской государственный технический университет, Россия

Тепловая задача при лазерной обработке

Оптимальные режимы лазерной обработки позволяют в полной мере использовать основные ее достоинства, а именно высокую степень концентрации энергии и максимальную эффективность ее применения.

Как найти критерий применимости лазера для обработки материалов в рамках принятого определения технологических лазеров, как тех, которые способны нагреть поверхность до заданной температуры Т ?.

Температура поверхность Т зависит от мощности Р, поглощенной единицей площади S: , где q так называемая плотность мощности, (W – энергия в импульсе, - длительность воздействия).

Соотношение между Т и плотность мощности q может быть определено из уравнений теплопроводности типа:

(1)

Где - оператор Лапласса = , Q – объемная плотность поглощенного светового потока, а – температуропроводность, - плотность, с – теплоемкость.

Чтобы решить уравнение (1) необходимо задать одно начальное условие, 6 граничных и определить Q(x,y,z,t).

(2)

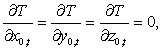
После решения системы этих уравнений связь между T и q выражается в виде:

Для металлов решение уравнения (1) при условиях (2) для круглого тепла – лазерного пятна с радиусом , будет:

. (3)

При (импульсный нагрев)

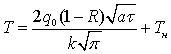(4)

При (непрерывный нагрев)

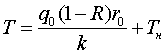(5)

Формулы (4) и (5) позволяют посчитать так называемую пороговую (критическую) плотность мощности , необходимую для нагревания до заданной температуры Т:

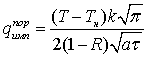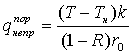(6) (7)

Аналитические решения нелинейных задач теории теплопроводности также осуществляют прямыми методами математического анализа. Эти методы можно успешно применять для расчетов тепловых процессов с учетом нелинейности теплофизических свойств.

Математическая модель процесса глубокого проплавления.

Пространственную нестационарную задачу теплопроводности в общем случае можно описать следующим уравнением:

(8)

Где Q – количество теплоты; - объемная теплоемкость; - тепловой поток; - коэффициент теплопроводности; G – расчетная область.

Задача лазерной обработки с глубоким проплавлением поставлена как симметричная относительной плоскости движения луча, и поэтому в качестве расчетной области G рассматривается половина образца.

Введем в математическую модель следующие расчетные области:

- область зоны прямого облучения (ЗПО) на передней стенке канала;

- область, примыкающая к ЗПО по ходу движения лазерного луча;

- область поверхностного источника факела;

- область канала проплавления.

Выделяемое количество теплоты Q определяется из теплового баланса

, (9)

Где

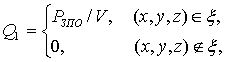
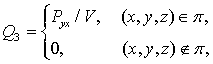
- элементарная площадка поверхности; V – элементарный объем.

Значения тепловых потоков вычисляем по формулам:

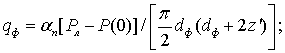
Для однозначной формулировки задачи математическую модель следует дополнить граничными условиями. В данном случае использовали граничные условия, соответствующие в теории теплопроводности третьей краевой задаче:

y=0 (из условия симметрии),

Где - коэффициент полной поверхностной теплоотдачи; T- температура окружающей среды; - граница тела.

Начальные условия, используемые в задачах:

Уравнения (8) описывают распространение теплоты в пределах какой-либо фазы (твердой и жидкой). На границе раздела фаз по тепловым потокам W действуют дополнительные условия:

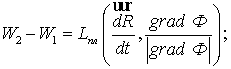
(10)

Где - скрытая теплота плавления; - положение границы фазового фронта; - уравнение границы фазового фронта.

Фазовый фронт определяется условием Т=Т*, где Т* - температура фазового перехода, индекс 1 относится к фазе с Т<T*, а индекс 2- к фазе с Т>T*.

Систему уравнений (8) при условии (10) на границе раздела фаза можно записать в однородном виде

Где - дельта-функция Дирака; - дивергенция теплового потока.

Список использованной литературы:

1. Григорьянц А.Г., Шиганов И.Н., Мисюров А.И. «Технологические процессы лазерной обработки». - М.: МГТУ им. Н.Э. Баумана, 2006г.

2. Лазерная и электронно-лучевая обработка материалов: Справочник / Н.Н. Рыкалин, А.А. Углов, И.В. Зуев и др. – М.: Машиностроение, 1985. – 496с.

3. Вейко В.П. «Технологические лазеры и лазерное излучение». – М.: СПбГУ ИТМО, 2006г. - 52с.