К.ф-м.н., доц. Гусев А.Ю., Панова В.И.

ГВУЗ «Национальный горный университет», Днепропетровск

Исследование плотности распределения интенсивности поступления пакетов в сети Интернет-провайдера

В данной статье рассмотрена методика вычисления плотностей распределения интенсивности поступления пакетов в сети Интернет-провайдера для различного количества пользователей.

Ключевые слова: плотность распределения, интенсивность поступления пакетов.

Введение

Сеть Интернет в Украине начала развиваться в первой половине 90-х годов XX-го века. С каждым годом можно было наблюдать колоссальный рост количества пользователей в сети Интернет. Увеличивалось и количество услуг предоставляемых Интернет–провайдером. Не всегда пользователь бывает доволен качеством услуг. Поэтому задача определения компромисса между стоимостью предоставляемых услуг и их качеством является актуальной.

Основная часть

Среди многих параметров, влияющих на качество Интернет-услуг, одним из наиболее важных является скорость гарантированной доставки Интернет-трафика пользователю, т.е. так называемая услуга CIR (Commitment Infjrmation Rate) [1]. Она представляет собой скорость передачи информации, которую гарантирует сеть при нормальных условиях. На практике все провайдеры услуг Интернет набирают клиентов так, что их суммарное значение CIR превышает скоростные возможности сети, и гарантируют CIR только с некоторой статистической вероятностью, что позволяет воспользоваться неравномерным характером трафика локальных сетей [2].

Задача данной работы заключается в вычислении плотностей распределения интенсивности поступления пакетов в сети Интернет-провайдера для различного количества пользователей, что позволяет эффективно распределять общую ширину полосы частот канала между различными пользователями. Суть метода состоит в следующем: Интернет - провайдер имеет общую полосу пропускания [0;G], бит/с. В его сети находятся n пользователей, между которыми он делит эту полосу в зависимости от того качества сервиса, которое заказал каждый из них и для передачи трафика каждому пользователю предоставляет следующие полосы:

[0; h₁], бит/с - первый пользователь,

[0; h₂], бит/с - второй пользователь,

...

[0; h_n], бит/с- n-ый пользователь.

В сети провайдера n пользователей и каждому из пользователей он выделяет максимальную полосу пропускания равную 100 Мбит/с.

Будем предполагать, что мгновенная скорость передачи является случайной величиной с равномерной плотностью вероятности на отрезке [m_i,100], Мбит/c –w(x) , где m_i– представляет собой минимальную скорость, на которой пользователь передает трафик Интернет – провайдеру и может принимать любое значение из интервала [0;100], Мбит/с.

Для определения суммарной функции плотности распределения n случайных величин используется аппарат характеристических функций. Функция плотности распределения суммы x_i ищется обратным преобразованием Фурье от характеристической функции:

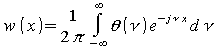
Графики функций плотностей распределений при различных n показаны на рис. 1 и рассчитаны при выбранных величинах минимальной скорости передачи трафика:; ; ; :

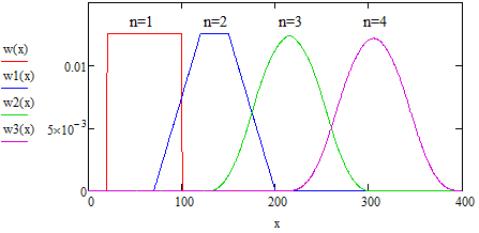
Рисунок 1 — График функции плотностей распределения для разного количества пользователей

Зная плотность можно определить интенсивность поступления пакетов . В случае ; ; ; .

Заключение

Результаты представленные на рис. 1 показывают, что чем больше пользователей находится в сети Интернет – провайдера, тем больше кривая функции плотности распределения стремится к нормальному закону распределения.

С помощью данной методики для рассмотренного выше примера, когда в сети Интернет – провайдера присутствует 1, 2, 3 и 4 пользователя, вычислены плотности распределения скорости поступления пакетов. Данная методика является универсальной и может применяться для вычисления плотностей распределения, а, следовательно, и максимальных интенсивностей поступлления пакетов, когда в сети Интернет - провайдера произвольное число пользователей.

Литература

1. E.A. Кучерявый. Управление трафиком и качество обслуживания в сети Интернет//СПб, Наука и Техника. 2004.

2. Вегешна Шринивас. Качество обслуживания в сетях IР / Вегешна Шринивас. - М.: Издательский дом «Вильямc», 2003. - 368 с.