Математика / 5. Математическое моделирование
Д-р. физ.- мат. наук Тумаев Е. Н.,
аспирант Шарай И. А.
Кубанский государственный университет
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ПРОИЗВОДСТВА НЕЙТРОФИЛОВ И МОНОЦИТОВ
Нейтрофилы и моноциты развиваются в
красном костном мозге из единого предка − колониеобразующей единицы
гранулоцитарно-макрофагального рядов (КОЕ-ГМ). В дальнейшем каждая клетка проходит через несколько
последовательных стадий развития. Так среди нейтрофилов выделяют следующие виды
клеток: колониеобразующая единица гранулоцитов (КОЕ-Г), миелобласт (НМб),
промиелоцит (НПм), миелоцит (НМ), метамиелоцит (НМм), палочкоядерный
нейтрофил (Пн), сегментоядерный
нейтрофил в костном мозге (Снкм), нейтрофил в крови (Снк) и нейтрофил в тканях
(Снт), а среди моноцитов: колониеобразующая единица моноцитов (КОЕ-М),
монобласт (Мб), промоноцит (Пм),
моноцит в крови (Мн) и макрофаг (Мф).
Целью данной работы является создание и
исследование математической модели нейтрофиломоноцитопоэза.
Для описания процессов деления в работе
используется логистическое уравнение. Расчеты кинетики переменных и решение
дифференциальных уравнений выполнено при помощи математического комплекса
MATHCAD 14.
Результаты
исследования
В соответствии схемой грануломоноцитопоэза
[1], была разработана система уравнений (1-15):
![]()
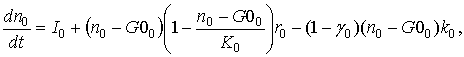 (1)
(1)
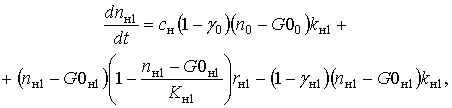 (2)
(2)
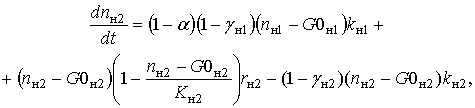 (3)
(3)
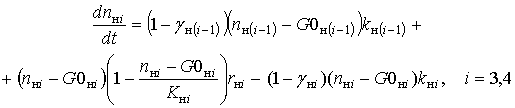 (4-5)
(4-5)
![]() (6)
(6)
![]() (7-10)
(7-10)
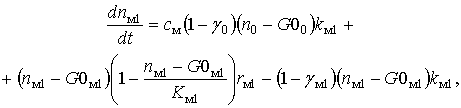 (11)
(11)
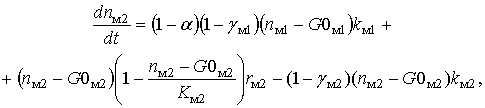 (12)
(12)
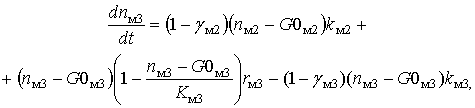 (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
где I0
– входящий поток клеток, G00 – концентрация КОЭ-ГМ в фазе обратимого
покоя, γ0 – коэффициент потери клеток КОЭ-ГМ путем апоптоза, сн – доля клеток КОЭ-ГМ
дифференцирующихся в нейтрофилы, см
– доля клеток КОЭ-ГМ дифференцирующихся в моноциты, k0 – скорость потока КОЭ-ГМ в следующую стадию, kнi – скорость потока нейтрофилов в следующую стадию, kмi – скорость потока моноцитов в следующую стадию, n0 – общая концентрация
КОЭ-ГМ, nнi – общая концентрация нейтрофилов на стадии созревания, nмi – общая концентрация моноцитов на стадии созревания, r0 – скорость роста КОЭ-ГМ, rнi – скорость роста
нейтрофилов на стадии, rмi – скорость роста моноцитов на стадии, K0 – поддерживающая
ёмкость среды для КОЭ-ГМ, Kнi – поддерживающая ёмкость среды для нейтрофилов на данной
стадии, Kмi – поддерживающая ёмкость среды для моноцитов на данной
стадии.
В таблицах 1-3 приведены численные
значения параметров модели при нормальном кроветворении, рассчитанные с учетом
[2-4]:
Таблица 1 – Данные по состоянию КОЕ-ГМ в норме.
|
n0 |
3,83 ∙ 105 |
r0, ч-1 |
0,19 |
|
G00 |
3,26 ∙ 105 |
K0 |
7,46 ∙ 104 |
|
k0, ч-1 |
0,046 |
I0, ч-1 |
39,99 |
|
сн |
0,88 |
см |
0,12 |
|
γ0 |
0,03 |
|
|
Таблица 2 – Данные по состоянию нейтрофилов в норме.
Таблица 3 – Данные по
состоянию моноцитов в норме.
|
|
nмi |
G0мi |
kмi, ч-1 |
rмi, ч-1 |
Kмi |
γмi |
|
КОЭ-М |
1,8 ∙ 106 |
1,5 ∙ 106 |
0,08 |
0,03 |
3,4 ∙ 105 |
0,03 |
|
Мб |
3,8 ∙ 107 |
3,2 ∙ 107 |
0,08 |
0,29 |
7,7 ∙ 106 |
|
|
Пм |
6,0 ∙ 108 |
5,1 ∙ 108 |
0,02 |
0,03 |
1,9 ∙ 108 |
|
|
Мн |
8,0 ∙ 107 |
- |
0,02 |
- |
- |
- |
|
Мф |
1,7 ∙ 109 |
- |
0,001 |
- |
- |
- |
Заключение
В работе предложена математическая модель
нейтрофиломоноцитопоэза, основанная на переходах клеток из одной стадии созревания
в другую. Благодаря большому числу параметров, в рамках данной модели можно
выделить факторы, влияющие на состояние конкретных элементов.
Список
литературы
1.
Ф.Дж. Шиффман,
Патофизиология крови. Пер. с англ. / Шиффман Ф.Дж. – М. – СПб. : Издательство
БИНОМ - Невский диалект, 2000. – 448 с.
2. Chadwick K., Shojaei
F., Gallacher L., Bhatia M. Smad7 alters cell fate decisions of human hematopoietic
repopulating cells // Blood. – 2005. – № 105. – P. 1905-1915.
3.
Нормальное кроветворение
и его регуляция / под ред. Н. А. Федорова. — М.: Медицина, 1976. — 544 с.
4.
Алмазов В. А., Афанасьев
Б. В., Зарицкий А. Ю. и др. Патофизиология. — Л. : Наука, 1979. — 232 с.