Математика/1.Дифференциальные и интегральные уравнения

Д.ф.-м.н. Городецький В. В., аспірант Тодоріко Т.С.

Чернівецький національний університет імені Юрія Федьковича,Україна

Багатоточкова нелокальна за часом задача для одного класу еволюційних псевдодиференціальних рівнянь

Метод побудови функцiональних просторiв нескiнченно диференцiйовних функцiй, заданих на ℝ, на якi накладаються певнi умови спадання на нескiнченностi та зростання похiдних iз збiльшенням порядку, був запропонований I.М. Гельфандом та Г.Є. Шиловим у монографiї [1]. Цi умови задаються за допомогою нерiвностей , {k, n} ⊂ ℤ₊, де – подвiйна послiдовнiсть додатних чисел. Якщо цi числа змiнюються довiльним чином разом з , то маємо простiр Л. Шварца S = S(ℝ) швидко спадних на ℝ функцiй. На сьогоднішній день найбiльш широко вивчено випадок, коли , де , – фiксованi параметри; при цьому, вiдповiднi простори позначають символом .

Випадок, коли , де та – монотонно зростаючi послiдовностi додатних чисел, якi задовольняють певнi умови (вiдповiднi простори позначають символом ) дослiджено в працi [2]. Встановлено, що в просторах визначенi i є неперервними оператори множення на x, на всi многочлени, на нескiнченно диференцiйовнi функцiї, якi задовольняють певнi умови, оператори диференцiювання, зсуву аргументу та розтягу. У даній роботі наведені результати дослідження iснування в просторах типу оператора диференцiювання "нескiнченного порядку" вигляду 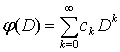, , побудованого за нескiнченно диференцiйовною функцiєю 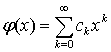. При цьому встановлено, що можна розумiти як псевдодиференцiальний оператор, побудований за аналiтичним символом. Також дослiджено нелокальну багатоточкову за часом задачу для еволюцiйного рiвняння з оператором у випадку, коли гранична функцiя є елементом простору типу та узагальненою функцiєю нескiнченного порядку типу ультрарозподiлiв (у просторах та топологiчно спряжених до них просторах вказана задача для еволюцiйних рiвнянь з оператором ранiше не дослiджувалась; детальний огляд праць, якi стосуються нелокальних задач для рiвнянь з частинними похiдними та диференцiально-операторних рiвнянь див. в [3]). При цьому, попередньо, вивчається структура та властивостi фундаментального розв’язку такої задачi, встановлюється її коректна розв’язнiсть у вiдповiдних просторах. Знайдено зображення розв’язку у виглядi згортки фундаментального розв’язку з граничною функцiєю.

Розглянемо послiдовнiсть {, n ∈ ℤ₊} додатних чисел, яка володiє властивостями: а) вона монотонно спадна; б) . За допомогою послiдовностi побудуємо послiдовнiсть за правилом: , n ∈ ℤ₊. Iз результатiв, наведених в [2] випливає, що послiдовнiсть задовольняє умови:

1) ℕ : ;

2) ℤ₊: ;

3) ℤ₊: ;

4) ℤ₊: ;

5) ℤ₊: .

Поруч розглянемо послiдовнiсть {, k ∈ ℤ₊} додатних чисел, яка також володiє властивостями а)-б) та послiдовнiсть {}. Символом позначимо сукупнiсть усiх функцiй ℂ^∞(ℝ), котрi задовольняють умову

∃c, A, B > 0 ∀{k, n} ⊂ ℤ₊ ∀x ∈ ℝ : .

Символом (ℂ) позначатимемо множину функцій, які є аналітичними продовженнями в ℂ функцій із класу . Більш детально простір (ℂ) описаний в [2].

Мультиплiкатором у просторi (ℂ) є кожна цiла функцiя , ℂ, яка задовольняє умову:

∀ε > 0 > 0: , z = x + iy ∈ ℂ.

Вiдповiдно, функцiя , x ∈ ℝ, є мультиплiкатором у просторi .

Символом позначатимемо простiр усiх лiнiйних неперервних функцiоналiв над вiдповiдним простором основних функцiй зi слабкою збiжнiстю, а його елементи називатимемо узагальненими функцiями. Якщо , то до цього ж простору належить також кожна похiдна , p ∈ ℕ (тобто елементи простору є нескiнченно диференцiйовними), зсув f(ay+b), , добуток αf, де α – мультиплiкатор у просторi основних функцiй.

Нехай 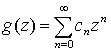, z ∈ ℂ, – деяка цiла функцiя. Говоритимемо, що в просторi (ℂ) задано оператор диференцiювання нескiнченного порядку 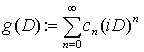, D = d/dz, якщо для довiльної функцiї (ℂ) ряд

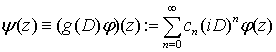, z ∈ ℂ,

зображає основну функцiю з простору (ℂ) (тут {} – послiдовнiсть, яка задовольняє умови 1) – 5)). Звуження оператора g(D) на простiр , яке позначатимемо символом , називатимемо диференцiальним оператором нескiнченного порядку в просторi . Правильним є наступне твердження.

Теорема 1. Якщо цiла функцiя g – мультиплiкатор у просторi (ℂ), то в цьому просторi визначений i неперервний оператор g(D), при цьому

, ℝ, . (1)

Зауваження 1. Якщо цiла функцiя 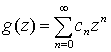, z ∈ ℂ, – мультиплiкатор у просторi (ℂ), то у просторi визначений i неперервний оператор g(D), при цьому для довiльної функцiї справджується рiвнiсть (1) (послiдовностi {} та {} такi, що функцiї γ та ρ, пов’язанi з цими послiдовностями, задовольняють умову , ).

Символом позначимо клас цiлих однозначних функцiй : ℂ → ℂ, якi є мультиплiкаторами в просторi (як функцiї змiнної x ∈ ℝ) i такими, що .

Якщо – мультиплiкатор у просторi , то для довiльної функцiї ψ ∈ , де маємо, що , бо , а функцiя , очевидно, є мультиплiкатором i в просторi . Тодi

.

Отже, псевдодиференцiальний оператор , побудований за функцiєю , визначений у кожному просторi , де , вiдображає цей простiр в себе i є неперервним; при цьому, з iншого боку, можна розумiти як диференцiальний оператор нескiнченного порядку, який дiє в просторi .

Для еволюцiйного рiвняння

, (t, x) ∈ (0, T] ×ℝ ≡ Ω, 0 < T < ∞, (2)

де , задамо багатоточкову нелокальну за часом задачу

, (3)

m ∈ ℕ, {, , …, } ⊂ (0, ∞), (, ..., ) ⊂ (0, T] – фiксованi числа, причому 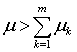, , , ℕ.

Класичний розв’язок ((0, T], ) задачi (2), (3) шукаємо за допомогою перетворення Фур’є у виглядi

Введемо позначення: , де

.

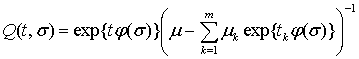Символом позначатимемо клас узагальнених функцiй з , якi є згортувачами в просторi .

Під час дослідження властивостей функції Q, як функції аргументу x, встановлено наступний наслідок.

Наслідок: Нехай , , де . Тоді в просторі справджується граничне співвідношення

.

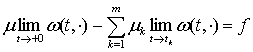Функція G є розвязком рівняння (2). Справді,

.

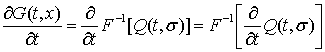З іншого боку,

.

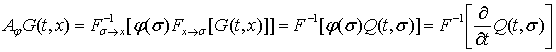Звідси вже випливає, що функція G задовольняє рівняння (2).

Надалi функцiю G називатимемо фундаментальним розв’язком багатоточкової (m-точкової) нелокальної за часом задачi для рiвняння (2).

З наведеного вище наслiдку випливає, що для рiвняння (2) m-точкову за часом задачу можна ставити так: знайти розв’язок рiвняння (2), який задовольняє умову

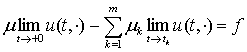, , (4)

де граничне спiввiдношення (4) розглядається в просторi (обмеження на параметри такi ж, як i у випадку задачi (2), (3)).

Теорема 2. Задача (2), (4) коректно розв’язна. Розв’язок дається формулою , , де G – фундаментальний розв’язок нелокальної багатоточкової за часом задачi для рiвняння (2).

Література:

1. Гельфанд И.М. Пространства основных и обобщенных функций / И.М. Гельфанд, Г.Е. Шилов. – М.: Физматгиз, 1958. – 307 с.

2. Городецький В.В. Задача Кошi та двоточкова задача для еволюцiйних рiвнянь iз операторами узагальненого диференцiювання / В.В. Городецький, О.В. Мартинюк // Доповiдi НАН України. – 2013. – № 3. – С. 7–13.

3. Нелокальнi крайовi задачi для рiвнянь iз частинними похiдними / [Пташник Б.Й., Iлькiв В.С., Кмiть I.Я., Полiщук В.М.]. – К.: Наукова думка, 2002. – 416 с.