к.ф.-м.н. Потёмин Г.В.

Нижегородский государственный технический университет им. Р.А. Алексеева

Дифференциально-геометрические скобки Пуассона третьего порядка на одномерном многообразии.

В работе изучены дифференциально-геометрические скобки Пуассона третьего порядка на одномерном многообразии M.

Ключевые слова: скобка Пуассона, метрика, связность, кручение, кривизна

Скобка Пуассона определяется для функционалов от полей Но, следуя принятому в теоретической физике формализму, её удобно записывать через «точечные функционалы», сосредоточенные на одном из полей в одной точке. Для одной пространственной переменной дифференциально-геометрическая скобка Пуассона третьего порядка на многообразии M имеет вид [1]:

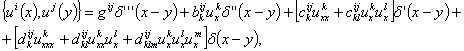
(1)

Здесь коэффициенты зависят только от координат , но не от их производных. Каждое слагаемое имеет степень однородности три относительно естественной градуировки

.

Рассмотрим общий случай: . При локальных преобразованиях переменных вида коэффициенты преобразуются как компоненты тензора типа (2,0), а величины

преобразуются как компоненты дифференциально-геометрических связностей.

В работах [2],[3] была доказана теорема о том, что «последняя связность» в скобке Пуассона (1) симметрична и имеет нулевую кривизну. Тогда существует такая система координат, в которой компоненты «последней связности» равны нулю. Такие локальные координаты определены с точностью до аффинных преобразований. В специальных координатах выполнены также условия:

.

Скобка Пуассона (1) принимает вид:

. (2)

Коэффициенты в (2) должны удовлетворять условиям:

(3)

(4) (5)

(6)

Скобку Пуассона (1) можно записать тогда в виде:

.

Условия (3)-(6) выглядят значительно проще для дифференциально-геометрических объектов с нижними индексами :

(7)

(8) (9)

(10)

Отсюда, в частности, следует, что метрика квадратично зависит от :

.

Такие пуассоновы структуры имеют важные и интересные нетривиальные приложения для некоторых нелинейных систем, например, уравнений Монжа-Ампера и уравнений ассоциативности двумерной топологической теории поля [4].

В доказательстве теоремы в работе [2] был пропущен случай N=1, т.е. когда соответствующий гамильтонов оператор является скалярным. Здесь этот пробел будет восполнен.

В скалярном случае скобку Пуассона можно записать:

- функции только переменной u.

Из условия кососимметричности скобки Пуассона получаем такие соотношения вместо (3):

(11)

Непосредственная проверка тождества Якоби даёт условия вместо (4)-(6):

и (12)

Тогда из (11) и (12) следует, что:

, ,

Окончательно, коэффициенты в скобке Пуассона третьего порядка в скалярном случае получаются:

,

, (13)

где g–произвольная функция от u(x).

Скобку Пуассона в этом случае принимает вид:

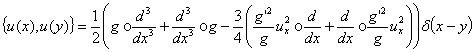
Литература.

1. Б.А. Дубровин, С.П. Новиков Гидродинамика слабо деформированных солитонных решёток. Дифференциальная геометрия и гамильтонова теория // УМН, 1989, т.44, вып.6, с.29-98

2. Г.В. Потёмин Некоторые вопросы дифференциальной геометрии и алгебраической геометрии в теории солитонов // Диссертация на соискание уч. степени канд. физ.-мат. наук. М.:МГУ, 1991

3. Г.В. Потёмин О дифференциально-геометрических скобках Пуассона третьего порядка // УМН, 1997, т.52, вып.3, с.173-174

4. E.V.Ferapontov, G.A.P.Galvao, O.I. Mokhov, Y. Nutku // Comm.Math.Phys. 1997, v.186, p.649-669