Современные информационные технологии/ 2. Вычислительная техника и программирование

Илипов М.М., к.ф.-м.н. Искакова А.С.

Евразийский национальный университет им. Л.Н. Гумилева, Казахстан

Вероятностное представление процесса выбора прецедента в системе Матлаб

Ранее в работе Прохорова М. Д. и Федунова Б.Е. [1] был введен алгоритм выбора прецедента при наблюдении ситуационного вектора с количественными координатами.

Пусть состояние ПрС/С описывается ситуационным вектором с координатами (х_{1, …}, x_n) и каждая координата х_i - лингвистическая переменная с множеством термов прецедентам (блок прецедента). Каждая строка матрицы представляет собой конкретный ситуационный вектор, при котором в прошлом успешно реализовался соответствующий прецедент.

Таблица 1

№ п/п	Координаты ситуационного вектора				Прецедент
	x1	x2	…	x n
					d1
:	:	:	:	:	:
					dm

Перенумеруем строки блока прецедента d_j двумя индексами: первый индекс – номер прецедента (здесь он является номером блока), второй индекс – порядковый номер ситуационного вектора в этом блоке.

Полученную упорядоченную таким образом систему логических высказываний называют нечёткой матрицей знаний или просто – матрицей знаний.

На основе текущих измерений точка формируется с количественными значениями его координат. Только в этой фиксированной точке в момент поступления замера и нужно определить значение функции принадлежности m_dj (x₁, .. x_i, .. x_n).

Допустим, что имеем прецедент d_j, который может быть получен из следующих возможных ситуационных векторов ,, …, .

Элементы множества W(d, z)={W(d, z₁), …, W(d, z_μ)} являются несмещенными оценками для вероятности , которые при j=1, …, μ определяются как

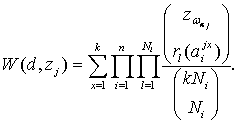
Итак, имеем множество несмещенных оценок вероятности проявлений искажений. Наиболее подходящая несмещенная оценка W(d, z_g) для вероятности оправдываемости метеорологического прогноза d P(D=d) распределения (3) определяется из всего множества полученных несмещенных оценок W(d, z)={W(d, z₁), …, W(d, z_μ)}, согласно определениям.

Решение z_g, основанное на наблюдении, является наиболее подходящим из множества z={z₁, … , z_m}, если

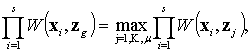(8)

где при i=1, … , s элементы множества W(x_i, z)={ W(x_i, z₁), … , W(x_i, z_m)} являются несмещенными оценками для вероятности P(D=d) распределения (3), определенными в (7).

Несмещенная оценка W(d, z_g) для вероятности P(D=d) распределения (1) является наиболее подходящей из всего множества несмещенных W(d, z)={W(d, z₁), …, W(d, z_μ)}, определяемых в (7), если z_g – наиболее подходящее решение, основанное на наблюдении.

Наиболее подходящая несмещенная оценка W(u, z_g) для вероятности P(U=u) модели является состоятельной, асимптотически нормальной и асимптотически эффективной.

Алгоритмическое решение нахождения наиболее подходящей несмещенной оценки в системе Матлаб представлены на рисунках 1-4.

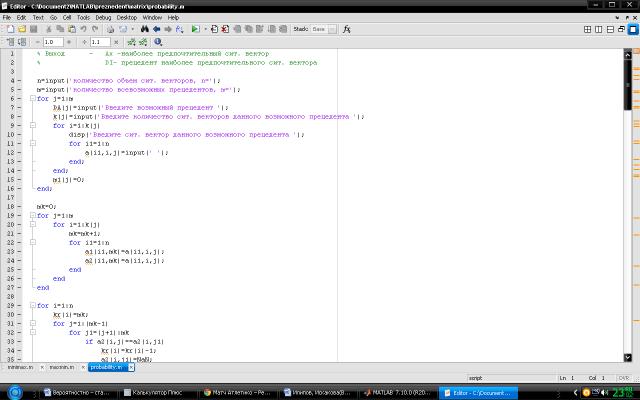\\Рис. 1

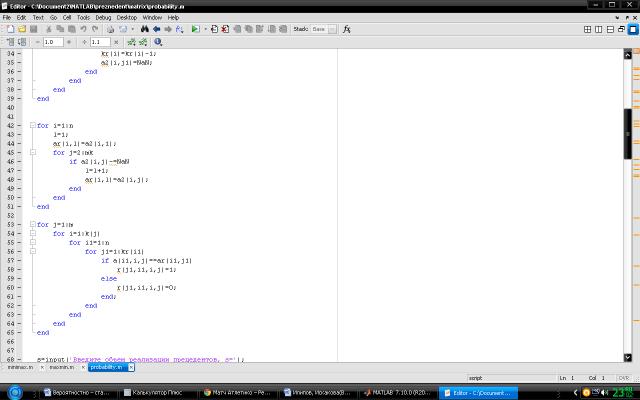
\\Рис. 2

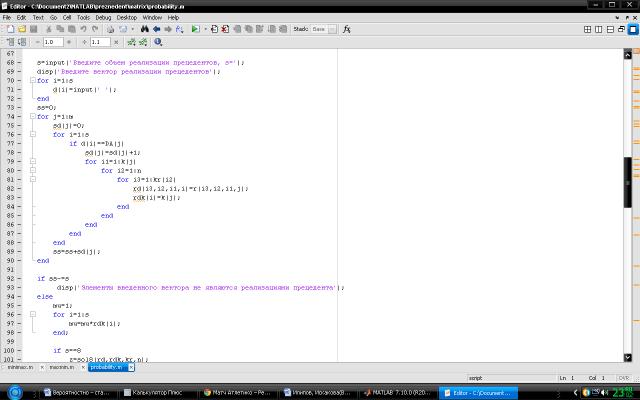
\\Рис.3

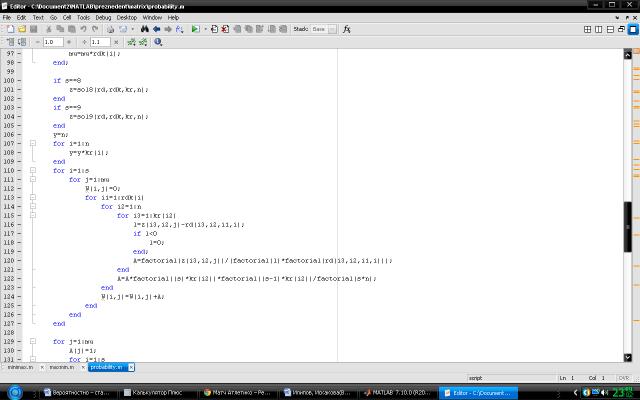
\\Рис. 4

Следует отметить, что основная часть результатов и методов, представленные в работе, могут быть использованы в научных исследованиях специалистами по математической статистике.

Литература:

1. Прохоров М. Д. Федунов Б.Е. Вывод по прецеденту в базах знаний бортовых интеллектуальных систем, размещаемых на борту антропоцентрических объектов.

2. Искакова А.С. Определение наиболее подходящей несмещенной оценки вероятности оправдываемости прогноза в метеорологии. // Сибирский журнал индустриальной математики. 2002 г.Том V, 1(9). С.79-84.

3. Риордан Д. Введение в комбинаторный анализ. М. 1963. – 287 с.

4. Савельев Л.Я. Комбинаторика и вероятность. М.: Наука. 1975.– 424с.

5. Крамер Г. Методы математической статистики. – М. 1975. – 648 c.