Математика/5. Математическое моделирование
к.ф.-м.н. доц. В.И. Евсеев ![]()
Казанский (Приволжский) федеральный университет, Казань, Россия,
кафедра прикладной информатики
УДК 681.32 1 - vladislaw.evseev@yandex.ru,
т.89047610772
МАТРИЧНОЕ МОДЕЛИРОВАНИЕ КВАДРАТИЧНЫХ
СТРУКТУР
§ 1. КВАДРАТИЧНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ.
Квадратичные логические
операции (сокращенно «квадра-операции») могут быть нескольких типов: дважды
бинарные и цепочные последовательности
(четырех типов). Кратко рассмотрим их
строение и методы вычисления. Отметим, что мы всюду применяем матричные
виды таблиц истинности, которые удачно раскрывают структуру этих операций. В общем случае матрица значений функции
истинности для квадра – операции имеет
вид
|
T |
0 |
0 |
1 |
1 |
|
|
Z |
Y X |
0 |
1 |
0 |
1 |
|
0 |
0 |
|
|
|
|
|
0 |
1 |
|
|
|
|
|
1 |
0 |
|
|
|
|
|
1 |
1 |
|
|
|
|
![]()
![]()
Для каждого типичного
случая таких операций матричная форма
таблицы истинности конкретизируется с учётом реального вида формулы.
Значения параметров операции принадлежат множеству {0;1}. Существует множество
типов квадра – операций. Рассмотрим
основные из них.
Дважды бинарные логические операции.
Они содержат две внутренние бинарные
операции, связанные одной внешней логической операцией, поэтому выражаются формулой:
![]() (1.1)
(1.1)
Каждую
часть следует сначала рассмотреть отдельно как бинарную операцию, затем, также
отдельно, построить внешнюю бинарную операцию, и лишь после этого соединить все
результаты в одну формулу. Рассмотрим
сначала первую внутреннюю бинарную операцию:
![]() (1.2).
(1.2).
Для неё получаем таблицу истинности:
|
Y X |
0 |
1 |
|
0 |
|
|
|
1 |
|
|
и
формулу рабочих блоков:
![]() (1.3)
(1.3)
Для
взаимной к ней операции получим:
![]() (1.4)
(1.4)
Аналогично
строится и вторая внутренняя бинарная операция: ![]() Для неё мы тоже
запишем таблицу истинности
Для неё мы тоже
запишем таблицу истинности
|
T Z |
0 |
1 |
|
0 |
|
|
|
1 |
|
|
и формулу рабочих блоков:
![]() . (1.5)
. (1.5)
Для взаимной к ней операции получаем формулу:
![]() . (1.6)
. (1.6)
Теперь строим внешнюю
бинарную операцию: ![]()
Для этой операции также
строим свою таблицу истинности
|
N M |
0 |
1 |
|
0 |
|
|
|
1 |
|
|
и формулу рабочих блоков:
![]() (1.7).
(1.7).
Обозначим выражения логических блоков квадра – операции в
виде матрицы ![]() Тогда для этой матрицы получаем таблицу:
Тогда для этой матрицы получаем таблицу:
|
i |
1 |
2 |
3 |
4 |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
Таким образом, символьный
массив квадра – операции можно представить
в виде
|
T Q |
0 |
0 |
1 |
1 |
|
|
Z |
Y X |
0 |
1 |
0 |
1 |
|
0 |
0 |
|
|
|
|
|
0 |
1 |
|
|
|
|
|
1 |
0 |
|
|
|
|
|
1 |
1 |
|
|
|
|
Значения выражений ![]() определяются как
произведения соответствующих высказываний или их отрицаний:
определяются как
произведения соответствующих высказываний или их отрицаний:
![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
,
![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() , (1.8)
, (1.8)
![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
,
![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() ,
, ![]() =
=![]() .
.
Кроме этого вида для квадра –
операций применяется структура «поля Канта»
|
Q |
|
|
||||||
|
|
|
|
|
|||||
|
|
|
0000 |
0100 |
0001 |
0101 |
|||
|
|
|
|
|
|||||
|
|
1000 |
1100 |
1001 |
1101 |
||||
Учитывая выражения для матриц истинности внутренних
операций, получим значения матрицы истинности
внешней бинарной операции, которую будем структурировать аналогично с
приведённым выше символьным массивом. При этом следует учитывать, что при
внешнем отрицании во внутренних операциях изменяется сам вид матриц истинности.
Таким образом, теперь мы находим явный
вид матрицы истинности квадра – операции, как алгебраической структуры,
соответствующей полю Канта (для рабочих блоков значения матрицы истинности равны
1, а для нерабочих они равны 0).
Примечание:
в конкретных задачах
изображение поля Канта упрощается, так как четырёхзначные шифры блоков не пишутся.
Матрица
![]() определяется через
значения матриц истинности двух внутренних и одной внешней бинарных операций:
определяется через
значения матриц истинности двух внутренних и одной внешней бинарных операций:
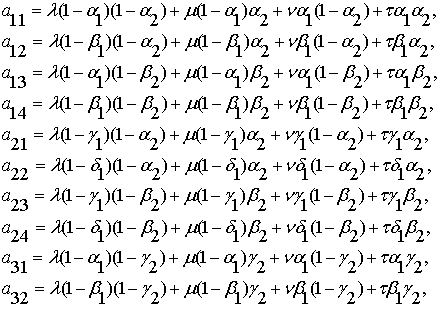 (1.9)
(1.9)
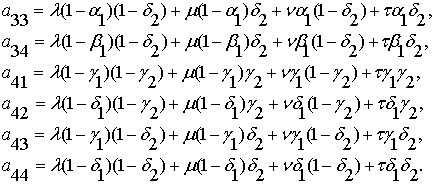
«Цепочные» квадратичные операции.
Существует четыре различных по смыслу
случая «цепочных» квадратичных операций:
а)
каждое последующее высказывание, кроме первых двух, объединённых внутренней
бинарной операцией, является внешним по
отношению к предыдущей формуле:
![]() (1.10)
(1.10)
б)
два внутренних высказывания объединены в одну операцию, а последнее
высказывание является внешним:
![]() (1.11)
(1.11)
в)
первое высказывание является внешним, а второе и третье объединены в одну
операцию:
![]() (1.12)
(1.12)
г)
Первое высказывание является внешним, а внутренняя бинарная операция объединяет
два последних высказывания:
![]() (1.13)
(1.13)
Рассмотрим
подробно первую из этих формул, а остальные
схемы аналогичны.
Итак, пусть известна «цепочная» квадра – операция первого вида.
Для неё получаем последовательность «вложенных»
бинарных операций:
![]()
Каждую
из этих операций анализируем как бинарную.
Мы
не будем записывать стандартные виды структуры четырех блоков каждой операции,
а сразу укажем виды рабочих блоков заданной и взаимной бинарных операций.
Для первой бинарной операции в этой цепочке получаем:
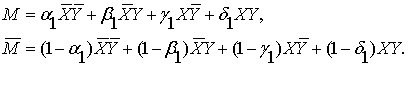 (1.14)
(1.14)
Аналогично находим для второй операции
этой цепочки:
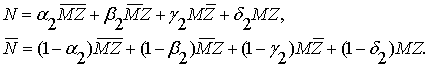 (1.15)
(1.15)
Третья
операция этой цепочки является финальной и рассматривается условно как внешняя.
Для
неё получаем исходное выражение:
![]() (1.16)
(1.16)
Промежуточную
операцию (N) проанализируем как тернарную операцию первого типа:
![]() (1.17)
(1.17)
Для неё получаем таблицу матрицы
истинности:
|
Z |
Y X |
0 |
1 |
|
0 0 |
0 |
|
|
|
1 |
|
|
|
|
1 |
0 |
|
|
|
1 |
|
|
Аналогично
строится таблица истинности для отрицания промежуточной операции (![]() ), из которой затем конструируется выражение для всей
операции Q. Мы приведём только вид матрицы
для отрицания промежуточной операции, а окончательную формулу можно записать в виде значений матрицы
истинности всей цепочной квадратичной операции. Взаимная к формуле (14.17)
операция
), из которой затем конструируется выражение для всей
операции Q. Мы приведём только вид матрицы
для отрицания промежуточной операции, а окончательную формулу можно записать в виде значений матрицы
истинности всей цепочной квадратичной операции. Взаимная к формуле (14.17)
операция ![]() имеет матрицу
истинности:
имеет матрицу
истинности:
|
Z |
Y X |
0 |
1 |
|
0 0 |
0 |
|
|
|
1 |
|
|
|
|
1 |
0 |
|
|
|
1 |
|
|
Полную запись всех значений матрицы
истинности в этом случае мы оставим читателям для самостоятельной работы.
Аналогично могут быть проанализированы
и другие виды «цепочных» квадратичных операций.
§ 2. СПЕЦИАЛЬНЫЕ ВИДЫ
СЛОЖНЫХ ВЫСКАЗЫВАНИЙ
1.К этой группе относятся: силлогизмы, полисиллогизмы,
эпихейремы, сориты, энтимемы, дилеммы и условные умозаключения. Мы
в данном пособии проведём изучение
только фигур силлогизма, суть которого
в установлении правильности (или наличия дефектов) структуры рабочих блоков.
Мы будем рассматривать фигуры
силлогизма в виде формализованной записи причинно-следственной цепочки
суждений. При этом их конструкции можно представить в следующем виде:
1 фигура силлогизма:
![]() (2.1)
(2.1)
2 фигура силлогизма:
![]() (2.2)
(2.2)
3 фигура силлогизма:
![]() (2.3)
(2.3)
4 фигура силлогизма:
![]() (2.4)
(2.4)
Каждая из этих фигур представляет собой
сложную тернарную операцию, для которой нужно построить совокупность рабочих
блоков и карту Карно или поле Канта для графической иллюстрации. В том случае,
когда арифметическая матрица истинности
не содержит нулевых блоков, фигура является законом логики
(тавтологией). В противном случае каждый нулевой элемент указывает на нерабочий
блок, который считается «дефектом» фигуры силлогизма. Проведём анализ каждой из
этих фигур.
2. 1 фигура.
Представляем
эту фигуру в виде последовательности бинарных операций:
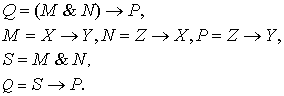
Теперь
записываем совокупности блоков данных бинарных операций и их отрицаний.
Для первой импликации получаем:
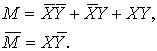
Для второй импликации – аналогично:
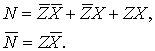
Также для третьей импликации:
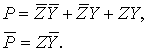
Вычисляем выражение в двойных скобках и
его отрицание:
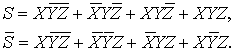
В результате находим выражение для всей
формулы:![]()
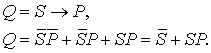
Подставляя в последнее выражение
значения соответствующих операций, находим:
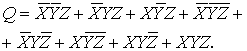
Итак,
в выражение ![]() входят все восемь
блоков универсума, поэтому первая
фигура силлогизма является законом логики (тавтологией).
входят все восемь
блоков универсума, поэтому первая
фигура силлогизма является законом логики (тавтологией).
3. 2 фигура.
В
данном случае получаем последовательность бинарных операций:
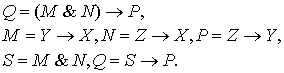
Для
внутренних бинарных операций и их отрицаний получаем:
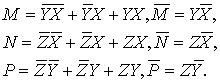
Поэтому для конъюнкции и её отрицания
находим:
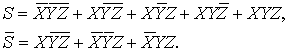
Таким образом, получаем рабочую
компоненту для всей операции:
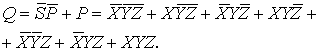
Значит, в данной формуле есть нерабочий
(дефектный) блок
![]()
Следовательно,
вторая фигура силлогизма не является законом логики и требует исправления
(преобразования к виду закона логики), которое будет указано в параграфе,
посвященном законам логики.
4. 3 фигура.
На
примере третьей фигуры силлогизма рассмотрим применение табличных методов. В
данном случае получаем
![]()
где обозначено
![]()
Выражение
Р следует преобразовать в эквивалентную форму с тремя переменными
![]()
Для
этой формы можно построить карту Карно с восемью рабочими блоками, которые
затем следует сравнивать с соответствующими блоками у выражения S.
Таким образом, для выражения ![]() получаем таблицу:
получаем таблицу:
|
Z |
Y X |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
Теперь
переходим к построению выражения S. Так
как
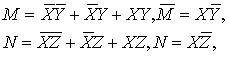
Получаем
по формуле для конъюнкции как логического произведения:
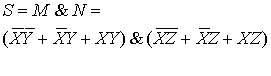
Поэтому,
после раскрытия скобок,
![]()
Значит,
для S получается таблица
|
Z |
Y X |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
Проведём
сравнение значений функции истинности для S и ![]() , учитывая, что логическое следование (импликация)
характеризуется требованием выполнения неравенств:
, учитывая, что логическое следование (импликация)
характеризуется требованием выполнения неравенств:
![]()
Это
неравенство нарушается только в блоке ![]() Поэтому указанный
блок оказывается «дефектом» рассмотренной фигуры силлогизма. Эта фигура также,
как и предыдущая, не является законом логики и требует исправления, которое
будет указано в параграфе, посвященном законам логики.
Поэтому указанный
блок оказывается «дефектом» рассмотренной фигуры силлогизма. Эта фигура также,
как и предыдущая, не является законом логики и требует исправления, которое
будет указано в параграфе, посвященном законам логики.
5. 4 фигура.
Для
четвёртой фигуры силлогизма получаем:
![]()
при
этом
![]()
Не
выписывая подробно промежуточные вычисления, сразу приведём вид выражения для S:
![]()
Значит, таблица Карно истинности для
этого выражения:
|
Z |
Y X |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
Сравнивая
таблицы для S и ![]() , приходим к выводу, что условия импликации, не выполняются
для двух дефектных блоков:
, приходим к выводу, что условия импликации, не выполняются
для двух дефектных блоков:
![]() и
и ![]()
поэтому
вторая, третья и четвертая фигура не
являются логическими законами, а их исправленный вид можно представить
формулами:
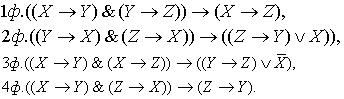 (2.5)
(2.5)
6.
Дадим теперь доказательство последней из приведённых формул силлогизма:
![]()
Заметим,
что в данном случае нужно доказать справедливость всей формулы (как
тавтологию). Для упрощения вычислений вводим обозначения:
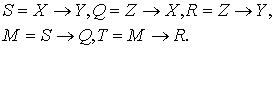
Малыми
латинскими буквами будем обозначать значения функции истинности соответствующих
высказываний. Так, получаем:
![]()
Последовательно
вычисляем значения m и t, учитывая идемпотентность функции истинности:
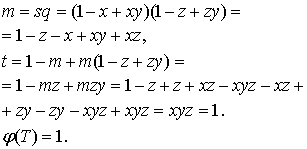
Это означает, что данная формула
является законом логики.
Заметим,
что только первая фигура силлогизма
совпадает с приведёнными законами, а вторая, третья и четвёртая фигуры изменены
для исключения дефектных блоков, присутствовавших в исходном виде.
7. Законы логики можно формулировать и
как правила вывода, тогда их доказательство можно проводить в табличной форме.
Рассмотрим в качестве примера доказательство второй формулы силлогизма (в виде
преобразованном к закону логики), которую запишем как правило вывода:
![]() (2.6)
(2.6)
Построим отдельно таблицы истинности тернарных операций,
указанных
в числителе и знаменателе.
Числитель
запишем в виде формулы:
![]()
Для него строим первичные матрицы:
![]()
![]()
|
X Y |
|
X |
|
|
1 |
1 |
|
Y |
|
1 |
|
X Z |
|
X |
|
|
1 |
1 |
|
Z |
|
1 |
По этим таблицам записываем рабочие
блоки:
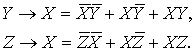
Эти выражения подставляем в формулу для
Q и, с учётом идемпотентности бинарных операций,
получаем:
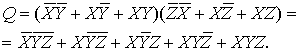
Таким образом, эта формула содержит
пять рабочих блоков.
Теперь
записываем матрицу построенной тернарной операции, как это делалось в § 7.
Во всех случаях сравнения формул будем считать порядок аргументов традиционным
(лексикографическим): {X,Y,Z}.
Приведём матрицу для формулы Q в числителе.
|
Z |
Y
X |
0 |
1 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
Аналогично
проводим анализ тернарной операции в знаменателе.
Здесь
внутренняя бинарная операция имеет вид:
![]()
Поэтому
получаем выражения для рабочих блоков:
![]()
Теперь
находим всё выражение для знаменателя:
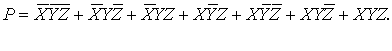
Для
выражения Р также строим таблицу истинности в форме Карно.
|
Z |
Y
X |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
Сравнение
таблиц истинности для Q и для Р приводит к выводу о выполнении и условий
импликации:
![]()
Таким образом, измененная формула для
второй фигуры силлогизма оказывается законом логики.
Аналогично могут быть доказаны и другие
логические законы.
Можно
сделать вывод, что применение матричных методов резко усиливает эффективность
исследования сложных логических формул.
ЛИТЕРАТУРА:
1. Ю.Л.Ершов, Е.А. Палютин. Математическая логика. СПб.
2005.
2. Дж.Шенфилд. Математическая логика. М.«Наука». 1975
3. Евсеев В.И. Логика. Монография. «ТАРИ». Казань. 2001.