Математика/5. Математическое моделирование

                            к.ф.-м.н. доц.  В.И. Евсеев  

Казанский  (Приволжский) федеральный университет, Казань, Россия,

                          кафедра прикладной информатики

   УДК 681.32                        1 - vladislaw.evseev@yandex.ru, т.89047610772

 

        ОБ ИССЛЕДОВАНИИ НОРМАЛЬНЫХ ФОРМ

 

§ 1.  НОРМАЛЬНЫЕ дизъюнктивные ФОРМЫ

 

         1.Рассмотрим сначала общее представление о нормальных формах.

Для их определения вводится символическая степенная функция

 

                                       ,                                          (1)

 

причем: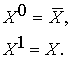                       

 

Для таких функций естественно определяются все ранее рассмотренные логические операции: если дан набор высказываний   то их элементарным конъюнктом (или конъюнктивным одночленом)  называется высказывание

                                     

                            .                  (2)

 

Аналогично, их элементарным дизъюнктом (или дизъюнктивным одночленом) называется высказывание вида

 

                                                (3)

 

Дизъюнкция конъюнктивных одночленов называется дизъюнктивной нормальной формой (д.н.ф.), её можно записать в виде формулы

 

                                                                   (4)

 

Аналогично, конъюнкция дизъюнктивных одночленов называется конъюнктивной нормальной формой (к.н.ф.), и её формула:

 

                                                                (5)

 

Заметим, что дизъюнктивная нормальная форма для трёх и четырёх переменных нами фактически использовалась при записи рабочих блоков в матрицах Карно. Конъюнктивная нормальная форма является её двойственным представлением и выглядит несколько искусственно. Эти нормальные формы применяются для синтеза микросхем.

         Нормальная форма называется совершенной, если в каждый её элементарный конструкт входят все исходные высказывания (возможно – с внутренними отрицаниями).

        

         2.Более подробно остановимся на случае тернарных нормальных форм.  В этом параграфе мы рассмотрим строение дизъюнктивных нормальных форм от трёх переменных. Для них мы получаем следующие слои элементарных конъюнктов:

а) одноместные конъюнкты

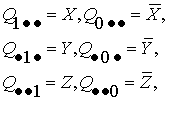                                                                      (6)

б) двуместные конъюнкты

 

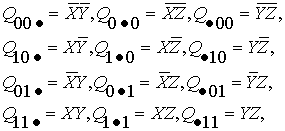                                              (7)

 

В) трёхместные конъюнкты

 

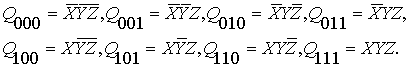                     (8)

 

 

Таким образом, любой тернарный  конъюнкт мы будем представлять в виде индексной записи   где индексы  принимают значения из множества  элементов . Поэтому тернарная дизъюнктивная нормальная форма имеет вид последовательности дизъюнкций:

 

                              (9)

 

Частным случаем дизъюнктивной нормальной формы является совершенная нормальная форма, в которой каждая переменная (высказывание) встречается в каждом элементарном конъюнкте только один раз (с отрицанием или без). Фактически для тернарных операций совершенная конъюнктивная форма состоит из всех рабочих блоков вида трёхместных конъюнктов (18.8).

         Для трёхместных тернарных конъюнктов вводится также сокращённая запись, соответствующая десятичной индексации (вместо двоичной). Применяя её, получим:

 

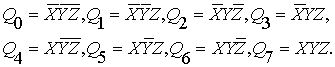                                     (10)

 

Именно такие выражения мы применяли для построения матриц Карно для тернарных операций и, в частности, полей Канта.

Заметим, что в некоторых сложных формулах могут появляться избыточные элементарные конъюнкты различного уровня, которые легко удалить при использовании матриц Карно. Кроме того, матрицы Карно позволяют решать вопрос о минимизации количества элементарных конъюнктов в какой-либо формуле: нужно представить заданную формулу в виде прямой суммы трёхместных элементарных конъюнктов, а затем выделять подобные члены, пользуясь законами логики. Мы рассмотрим эти методы на примерах.

3. Чтобы не загромождать запись многочисленными скобками, мы будем пользоваться традиционным представлением о порядке выполнения бинарных операций: если не выставлены скобки, то выполняются сначала все конъюнкции в элементарных конъюнктах, затем они последовательно соединяются дизъюнкциями. Отметим, что отрицания легко переносятся к самим внутренним высказываниям с помощью законов да Моргана. Если в исходной формуле присутствуют какие-либо другие операции, то с помощью законов взаимосвязи между бинарными операциями все они приводятся к формулам, содержащим конъюнкции, дизъюнкции и их отрицания. Отметим, что традиционно считается, что противоречивая исходно формула не имеет дизъюнктивной нормальной формы, хотя в реальности эта форма – просто нулевая, так как отсутствуют рабочие блоки на карте (или в матрице) Карно.

Теперь перейдём к некоторым примерам.

3.1. Пусть задана исходная формула

 

                                                   (11)

 

Эта формула – только от двух переменных, поэтому в её преобразовании будут принимать участие элементарные конъюнкты первого и второго уровней. Представим исходную формулу в виде конъюнкции двух высказываний:

 

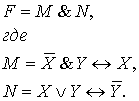                                                                            (12)

 

Для этих выражений по формулам бинарных операций получаем:

 

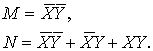                                                                         (13)

Следовательно, их конъюнкция имеет вид

                  

                            ,                                                            

 

Что приводит к выводу о виде ДНФ:

 

                                                                                       (14)

 

3.2. Задана формула

 

                                         (15)

 

Требуется построить для неё ДНФ.

 

Для решения подразделяем всю исходную формулу на две части:

 

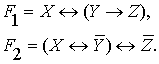                                                                        (16)

 

В первой формуле вводим обозначение  .

 

Теперь получаем

 

                  

 

Поэтому

 

                                                        (17)

 

Для этой формулы построим матрицу Карно:

 

                  

Z

 

       Y 

X

 0

1   

0

 0

0

1

0

 1

1

0

1

 0

0

0

1

 1

1

1

                           

 

 

 

 

 

 

 

 

 

 

 

Аналогично проводится преобразование второй формулы. Для этого вводится обозначение внутренней бинарной операции 

В этом случае находим

 

                 

Поэтому

 

                                                       (18)

Значит, для неё матрица Карно имеет вид

 

 

Z

 

       Y 

X

 0

1   

0

 0

1

0

0

 1

0

1

1

 0

0

1

1

 1

1

0

 

                           

 

 

 

 

 

 

 

 

 

 

Замечаем, что для построения импликации составляющих формул нужно знать их отрицания, которые находятся или непосредственно  (вычитанием из общей формулы универсума), или с помощью построения матриц Карно. Мы применим первый способ, и получим:

 

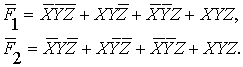                                                      (19)

Окончательная формула представляет собой импликацию, в которой

 

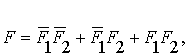
подставляя найденные выражения, получаем:

 

                                             (20)

 

         Для неё также построим матрицу Карно

 

Z

 

       Y 

X

 0

1   

0

 0

1

0

0

 1

0

1

1

 0

1

0

1

 1

1

1

        

                           

 

 

 

 

 

 

 

 

        

 

 

Данная формула представляет собой вид совершенной дизъюнктивной формы.

         Заметим, что полученная формула не является тавтологией (всюду истинной формулой), хотя оказывается выполнимой.

 

 

         § 2. КОНЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ

 

         1. Сразу перейдём к рассмотрению тернарных конъюнктивных нормальных форм, как наиболее значимых в учебном процессе. Элементарные дизъюнкты, из которых будут составляться конъюнктивные нормальные формы, обозначим по аналогии с предыдущими обозначениями для элементарных  конъюнктов, полагая:

        

         а) для одноместных дизъюнктов

 

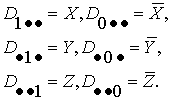                                                                     (21)

 

         б) для двуместных дизъюнктов

 

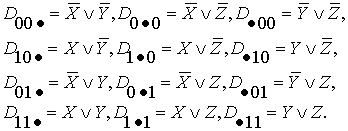                                  (22)              

 

         в) для трёхместных дизъюнктов

 

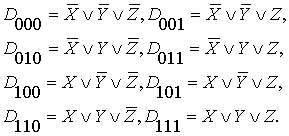                                             (23)

 

 

         Таким образом, тернарная  конъюнктивная нормальная форма может быть представлена в виде последовательности конъюнкций:

 

                                     (24).

 

Здесь параметры  принимают значения из множества

 

         Если все входящие в данную формулу элементарные дизъюнкты являются трехместными, то сама форма называется совершенной.

         2. Для трёхместных конъюнктов  также применяются сокращённые обозначения, в которых используются десятичные эквиваленты двоичной записи   индексов, что приводит к виду:  

 

                  

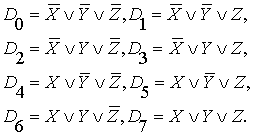                                                     (25)

         По законам двойственности конъюнкции и дизъюнкции мы можем сопоставить элементарным дизъюнктам соответствующие им элементарные конъюнкты, учитывая законы де Моргана:

 

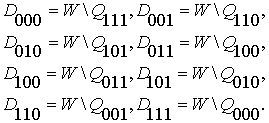                                                  (26)

 

В упрощенной записи эти формулы имеют вид:

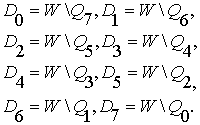                                                                (27)

 

         Аналогично может быть найдена взаимосвязь между любыми уровнями конъюнктов и дизъюнктов.

Затем строятся соответствующие внешние конъюнкции  для получения конъюнктивной нормальной формы.

         3. Рассмотрим несколько поясняющих примеров.

3.1. Найти  ДНФ и КНФ для тернарной операции:

 

                                                                            (28)

 

Сначала строим дизъюнктивную нормальную форму. Для этого вводим обозначение внутренней бинарной операции

 

                    

         Для внутренней бинарной операции находим по формулам дизъюнкции

 

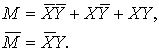                                                                        (29)

 

 

Поэтому для всей формулы получаем

 

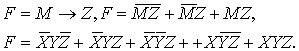                                            (30)

 

Последняя из формул (19.9) является   дизъюнктивной нормальной формой и может быть записана в виде

 

                                          (31)

 

В упрощенной записи эта формула записывается так:

 

                                                            (32)

 

Теперь составляем для неё матрицу Карно:

 

                  

Z

 

       Y 

X

 0

1   

0

 0

0

1

0

 1

1

0

1

 0

1

1

1

 1

0

1

        

                           

 

 

 

 

 

 

 

 

 

        

Отсюда делаем вывод о наличии нулевых блоков, на базе которых можно перейти к построению конъюнктивной нормальной формы, учитывая формулы (19.6):

 

Таким образом, получаем вид совершенной конъюнктивной нормальной формы для данной формулы:

 

                                                                (33)

 

В упрощенной записи находим:

 

                                                                           (34)

 

Или – в явном виде:

 

                                  (35)

 

3.2. Найдём обе нормальные формы для формулы:

 

                                                                   (36)

 

Сначала ищем дизъюнктивную нормальную форму. Для этого вводим обозначения бинарных операций:

 

                                                (37)

 

Для них находим выражения через конъюнкции по соответствующим формулам бинарных операций. При этом сразу записываем сами формулы

 

и их отрицания:

 

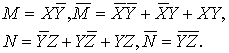                                                          (38)

 

Теперь для всей формулы получаем:

 

                                                                      (39)

 

При вычислении результата следует учитывать, что конъюнкции одинаковых элементов объединяются в один, а для противоположных (отрицаний) дают пустое множество, то есть, исключаются из формулы.

         Таким образом, получаем:

 

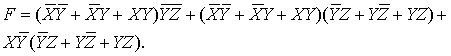             (40)

 

После раскрытия скобок и приведения подобных членов, находим:

 

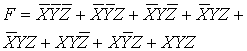                                                      (41)

 

         Записываем матрицу Карно для этой формулы:

 

                           

        

Z

 

       Y 

X

 0

1   

0

 0

1

1

0

 1

0

1

1

 0

1

1

1

 1

1

1

        

                           

 

 

 

 

 

 

 

 

 

 

         Таким образом, приходим к выводу, что

 

                                                                                   (42)

         Поэтому сразу можем записать конъюнктивную нормальную форму:

 

                            .                                                   (43)

 

                   Таким образом,  можно сделать вывод, что на базе матрицы Карно просто можно найти все виды нормальных форм.

 

ЛИТЕРАТУРА:

 

 

1.     Ю.Л.Ершов, Е.А. Палютин. Математическая логика. СПб. 2005.

2.     Дж.Шенфилд. Математическая логика. М.«Наука». 1975

3.     Евсеев В.И. Логика. Монография. «ТАРИ». Казань. 2001.