Божанов Е.Т., Касымбекова М.Т., Скакова А.Б., Койшыбаева Ж.Ж.
Казахский
национальный технический университет им. К.И. Сатпаева
ДВИЖЕНИЕ НЕФТИГАЗОВОЙ СМЕСИ ПО НЕФТИГАЗОВЫМ ТРУБАМ ПОД
ДЕЙСТВИЕМ КРИТИЧЕСКОЙ СИЛЫ ![]() , КОГДА ФОРМА ПОПЕРЕЧНОГО СЕЧЕНИЯ КОНУСОИДАЛЬНОГО ТИПА,
ЛЕЖАЩАЯ НА ОСНОВАНИИ ТИПА ВИНКЛЕРА
, КОГДА ФОРМА ПОПЕРЕЧНОГО СЕЧЕНИЯ КОНУСОИДАЛЬНОГО ТИПА,
ЛЕЖАЩАЯ НА ОСНОВАНИИ ТИПА ВИНКЛЕРА
Постановка
задачи
Пусть
математико-гидродинамическое моделирование резервуара, лежащего на основании
типа Винклера под действием критической силы ![]() приводит к дифференциальному уравнению изогнутой оси
поперечного сечения резервуара [1]-[4] к
виду:
приводит к дифференциальному уравнению изогнутой оси
поперечного сечения резервуара [1]-[4] к
виду:
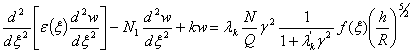 ,
,
![]() (I)
(I)
Нагрузку
упруго-вязкой среды со стороны нефтяной смеси представим в виде модели Фоихта
![]() (1)
(1)
Изменение
плотности поперечного сечения резервуара на отрезке ![]()
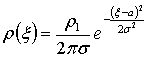 (2)
(2)
Где
![]() ;
; ![]() ;
; ![]()
При
предположениях ![]() ,
,
![]()
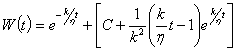 при
при ![]() (3)
(3)
В
следующих случаях:
А) –
случай. ![]() ;
;![]() ;
; ![]() ;
;
В) –
случай. ![]() ;
;![]() ;
; ![]() ;
; ![]() ;
;
С) –
случай. ![]() ;
;![]() ;
; ![]() ;
; ![]() ;
;
1. Рассмотрим первое
уравнение системы в случае А).
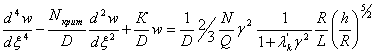 ,
,
![]() (4)
(4)
При
граничных условиях:
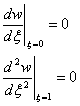
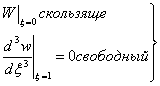 (5)
(5)
![]() ;
; 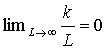 .
.
![]() (6)
(6)
На
оснавании граничных условии (5)
решая аналогичным образом задачи (4) получим:
![]() (7)
(7)
Здесь
![]() (8)
(8)
![]() ;
; 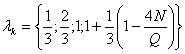 (9)
(9)
![]() ;
; ![]()
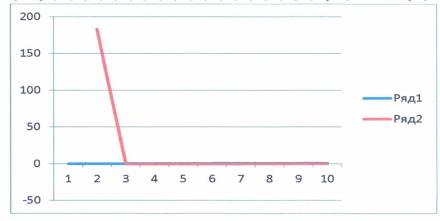
Построить
график функции из формулы (7)- (9) при следующих данных:
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]()
|
|
Построить
график функции ![]() из уравнения (7)- (9) при следующих данных:
из уравнения (7)- (9) при следующих данных:
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
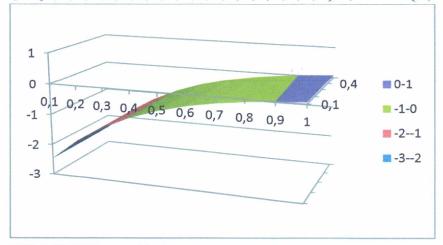
Построить
график функции ![]() из уравнения (7)- (9) при следующих данных:
из уравнения (7)- (9) при следующих данных:
![]() ;
;![]() ;
;![]() ;
; ![]() ;
;![]() ;
; 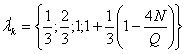 ;
;
![]() ;
; ![]() ;
; ![]()
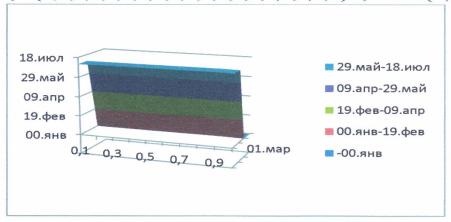
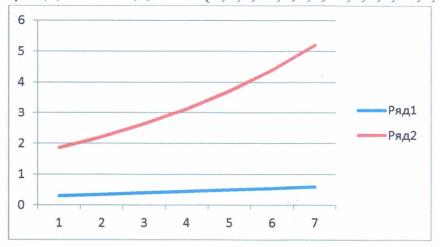
Построить
график функции ![]() из уравнения (4) при следующих данных:
из уравнения (4) при следующих данных:
![]()
![]() ;
; ![]() ;
; ![]() ;
;
2. Рассмотрим первое
уравнение системы в случае В).
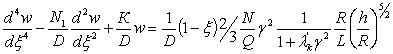 ,
,
![]()
![]() (10)
(10)
При
граничных условиях:
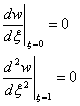
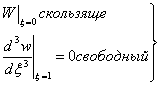 (11)
(11)
Решение:
Корни
характеристического уравнения ![]()
![]() ;
;![]() ;
;![]()
![]() ;
; ![]() ;
; ![]() ;
;
Общее
решение:
![]()
![]()
На
основании (10) из (11) получим:
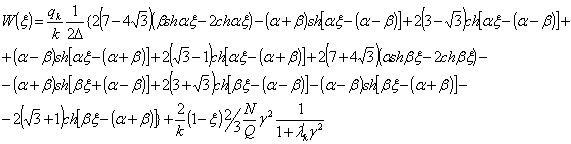
(12)
Здесь ![]()
![]() ;
; 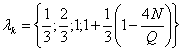 ; (13)
; (13)
![]() ;
; ![]() ;
; ![]() ;
;![]() ;
;
![]() ;
; ![]() ; (14)
; (14)
Построить
график функции из формул (12)-
(14) при следующих данных:
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]() ;
;
![]() ;
; ![]() ;
;
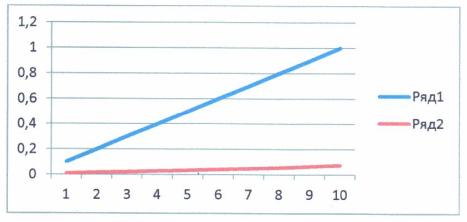
Построить
график функции ![]() из уравнения (12)- (14) при следующих данных:
из уравнения (12)- (14) при следующих данных:![]() ;
; ![]() ;
;![]() ;
;
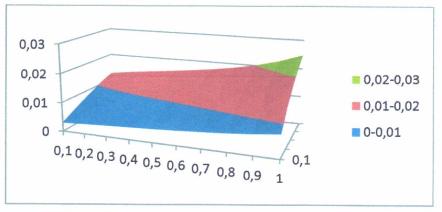
Построить
график функции ![]() из уравнения (12)- (14) при следующих данных:
из уравнения (12)- (14) при следующих данных:![]() ;
; ![]() ;
;![]() ;
;
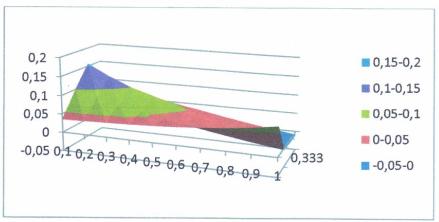
Построить
график функции ![]() из уравнения (10) при следующих данных:
из уравнения (10) при следующих данных:![]() ;
; ![]() ;
;![]()
![]() ;
; ![]() .
.
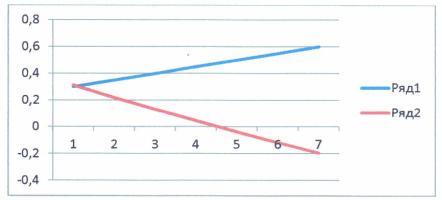
3.
Рассмотрим первое уравнение системы в случае С
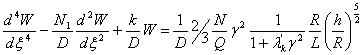 ;
; ![]() ; (15)
; (15)
Замечание №1. Движение нефтегазовой смеси по трубам от одной насосовой станции к другой
по трем зонам [5],[6] должна быть плавно
изменяющиеся, однако невозможно избежать разницы деформации в местах стыка или
сопряжения.
При
граничных условиях:
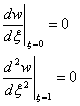
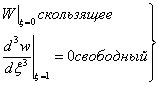
![]() ;
; ![]() ; (16)
; (16)
Решение:
Корни
характеристического уравнения
![]()
![]() ;
; ![]() ;
;![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;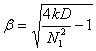 ;
; ![]() ;
; ![]() ;
;
Общее
решение(15) (линейное перемещение):
![]() ; (17)
; (17)
На
основании (16) из (17) получим:
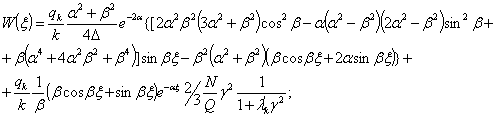 (18)
(18)
Здесь:
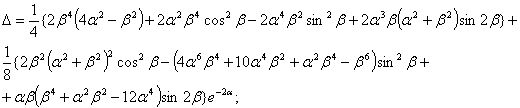 (19)
(19)
![]() ;
; ![]() ; (20)
; (20)
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
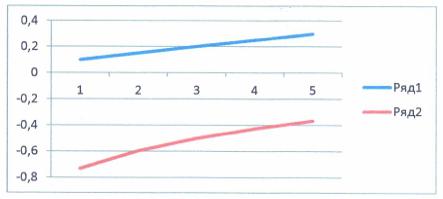
Построить график
функции из формул (18)-(20) при следующих данных:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
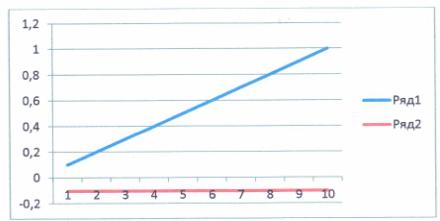
Построить график
функции ![]() из уравнения(18)-(20) при следующих данных:
из уравнения(18)-(20) при следующих данных:
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
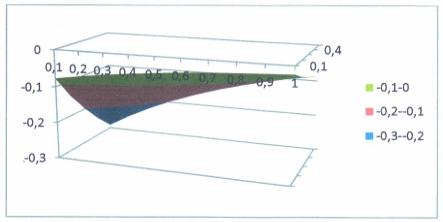
Построить график
функции ![]() из уравнения (18)- (20) при следующих данных:
из уравнения (18)- (20) при следующих данных:
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
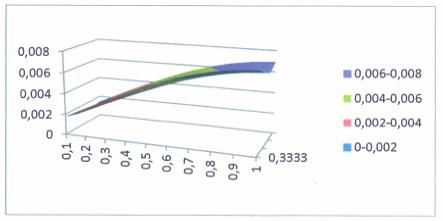
Построить график
функции ![]() из уравнения (15)
при следующих данных:
из уравнения (15)
при следующих данных:![]() ;
;![]()
Введем обозначения: ![]() ;
; ![]() - новые физико-механические
харатеристика материала, то
- новые физико-механические
харатеристика материала, то
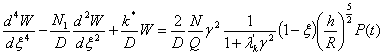 ;
;
![]() .
.
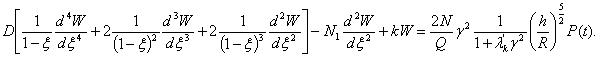
ЛИТЕРАТУРА
[1]. Божанов Е.Т.,Ибраимкулов
А.М., и др. “Напряженно-деформируемое
состояние и устойчивость нефтегазопроводов при действии линейно изменяющегося
по длине поперечного давления со стороны упругого заполнителя, треугольной
эиюры ”, Вестник КазНТУ, №2(52), Алматы, 2006г.
[2]. Божанов Е.Т., Ибраимкулов А.М., Жаканова А., Дмитриева Н. “Исследование проблем устойчивости и выпучивания композитов из чередующих двух “бутербодов” под действием критической силы по теориям М.А. Био, В.В. Новожилов, А.Н. Гузь, Л.С.Лейбензони А.Ю. Ишлинский”,Труды международной научно-практической конференции “Информационные и телекоммуникационные технологии”, том II, Алматы, 2012г.
[3]. Божанов Е.Т., Ибраимкулов А.М., Скакова А.Б.“Об одной математической модели технологии разработки нефтяных месторождении из N-го горизонта из 4-х чередующих приведенных слоев ”,Труды II-ой международной научной конференции, “Высокие технологии–залог устойчивого развития”, том II, Алматы, 2013г.
[4]. Божанов Е.Т., Ибраимкулов А.М., Койшыбаева Ж.Ж., Мусаева Ж.К. “Выпучивание симуляционной модели резервуара в зависимости от вида критической силы по форме критической деформации треугольного вида поперечного сечения ”, Материалы за IX-международная научна практична конференция, “Бъдещетовъпроси от света на науката - 2013”,Том 33, Математика, Физика, София, “Бял ГРАД-БГ” ООД 2013.
[5]. Божанов Е.Т., Отарбаев Ж.О., Буганбаева С.Н. “Механико-математическое моделирование нефтепроводов, транспортирующих вязкие нефти методом горячей перекачки”, Труды международного форума “Наука и инженерное образование без границ”, КазНТУ, том I, Алматы, 2009г.
[6]. Божанов Е.Т., Джунисов А.Т., Акимжанова Ш.А. “Математическая модель движения нефтигазовой смеси по стволам траектории скважины под действием технологического критического давления в N-ом горизонте гомогенного пласта большой мощности”, Труды II-международной научной конференции “Высшие технологии – залог устойчивого развития”, КазНТУ, том II, Алматы, 2013г.