ОПРЕДЕЛЕНИЕ КРИТИЧЕСКИХ ДЕФОРМАЦИЙ

ПРИ УДАРЕ ОБОЛОЧКИ НА УПРУГУЮ ПОВЕРХНОСТЬ

Голованов О.А., Данилов А.М.

При падении эллипсообразной стальной оболочки толщиной B с массой m и габаритными размерами a, b с высоты h на идеально упругую поверхность возникают деформации [1]. Определим критическое значение высоты падения , при котором деформации превышают допустимые. Решение этой задачи не является тривиальным и сводится к решению системы:

,

(первое уравнение есть уравнение неразрывности, второе – уравнение движения; F - плотность массовых сил, G - тензор напряжений; - плотность среды, u - скорость частиц) при соответствующих начальных и краевых условиях.

Известно, при приемлемых допущениях задача о критических нагрузках в оболочке упрощается и сводится к задаче об устойчивости решения обыкновенного дифференциального уравнения (при нулевых граничных условиях ):

, ,

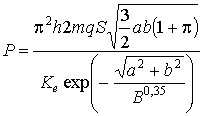S - площадь удара, - эмпирический коэффициент, учитывающий физические свойства стальной оболочки и ее геометрию; q - ускорение свободного падения.

Дифференциальное уравнение заменой сводится к интегральному уравнению

,

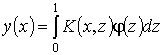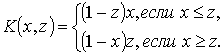- функция Грина оператора при нулевых граничных условиях.

Справедливо .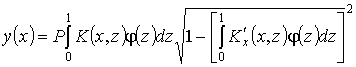

Это уравнение имеет нулевое решение при всех значениях параметра . При некоторых P интегральное уравнение может иметь ненулевые решения, которыми определяются формы потери устойчивости оболочки. Значение параметра - называют критическим, если при некоторых, близких к значениях параметра R . уравнение имеет малые ненулевые решения. Иначе говоря, критическое значение параметра - это точка бифуркации для интегрального уравнения.

Полученное интегральное уравнение можно рассматривать как операторное уравнение вида с вполне непрерывным оператором в пространстве, элементами которого являются непрерывные и ограниченные функции на всей числовой прямой. Линеаризация интегрального уравнения приводит к уравнению

.

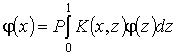Если - ненулевое решение этого уравнения при , то функция

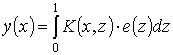
будет решением уравнения

,

удовлетворяющим нулевым граничным условиям. Отсюда вытекает, что каждое характеристическое значение линеаризованного уравнения является простым и, следовательно, является точкой бифуркации. Соответствующие значения R дают критические деформации. Ненулевые решения появляются при .

Учитывая, что собственные значения равны , получаем величину критической высоты

.

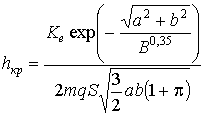При происходит потеря устойчивости в оболочке (оболочка деформируется).

Известно, если нагрузка превышает критическую в 10-20 раз, то происходит разрушение оболочки. Сила удара при падении оболочки на идеально упругую поверхность пропорциональна высоте h, следовательно, процесс разрушения наступит, если . Для высоты падения можно указать вероятность разрушения боеприпаса равной . Промежуточные значения можно аппроксимировать зависимостью

,

где a - коэффициент роста функции.

Литература

1. Плющ А. А., Голованов О. А., Данилов А. М., Гарькина И. А. Обобщенная математическая модель управления безопасностью арсеналов и баз хранения боеприпасов // Вісник Хмельницького національного університету. Технiчнi науки. –№ 1. – 2007. – С. 241-246.