МОДЕЛИРОВАНИЕ РАЗРУШЕНИЯ КОРПУСОВ ИЗДЕЛИЙ

ОТ КОРРОЗИОННЫХ ПРОЦЕССОВ

Гарькина И.А., Голованов О.А.

Рассматривается объект уничтожения химического оружия (ОУХО), которая, как и любая другая сложная система, не может обладать абсолютной безопасностью. Моделирование такой системы требует междисциплинарных исследований с преодолением неопределенностей целей на основе системного анализа [1]. Однако это не означает, что при проектировании ОУХО могут быть допущены возможности возникновения при эксплуатации очень тяжелых аварий. К основным задачам безопасности ОУХО относятся задачи обоснования количественных требований к безопасности и создания методов расчета на безопасность. Логическая схема моделирования хранения и уничтожения химического оружия предусматривает междисциплинарный подход, каждый блок которой относится к одной из логических подсистем:

- «Моделирование технологического процесса» - имитационное моделирование процесса уничтожения химического оружия (авиационных химических боеприпасов);

- «Моделирование заражения» - определение зон заражения;

- «Моделирование разрушения» - математическое моделирование критических деформаций авиационных химических боеприпасов в условиях хранения и транспортировки.

Ограничимся вопросом моделирования разрушения корпусов авиационных бомб от коррозионных процессов. Построим вероятностную модель разрушения оболочки боеприпаса от коррозии. Будем полагать, что разрушение происходит на одинаковую в глубину по всей поверхности оболочки (плотность металла - g ). Это позволяет использовать локальную модель для одного направления. Процесс коррозии рассматривается как переход от состояния оболочки, характеризуемого проникновением коррозии на глубину x к состоянию оболочки, характеризуемого проникновением коррозии на глубину (– размер элементарного участка, подвергшегося разрушению коррозией). Предполагается, вероятность разрушения оболочки зависит от величины x участка оболочки и не зависит от места его расположения. Примем, что величина х пропорциональна времени (; процесс разрушения можно рассматривать как стационарный во времени). Вероятность наступления больше одного события, приводящего к разрушению оболочки на элементарном участке , примем равной нулю (ординарность). Наконец, вероятность разрушения оболочки на участке , примем равной (l - определяет интенсивность случайного потока событий отнесенного к единице длины (простейший поток)). При относительно равномерном типе коррозионного разрушения Скорость коррозии выразим известным весовым показателем К коррозии (принимается равным весу металла (в граммах), превращенного в продукты коррозии за единицу времени (час или сутки) с единицы его поверхности (м² или дм²)). Иногда скорость коррозии выражают также глубинным показателем П коррозии (среднее проникновение коррозионного разрушения в металл (в миллиметрах) за единицу времени (1 год)). Указанные показатели коррозии связаны соотношением: .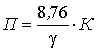

Пусть В₀ - толщина оболочки в начальный момент времени. В момент времени t толщина оболочки будет . Вероятность разрушения при B=B₀ примем равной p₀, а вероятность разрушения W(B)|_B=0=1. При вероятности W(x) разрушения в точке x (соответствует глубине проникновения коррозии на глубину x) вероятность отсутствия разрушений будет . С учетом условий однородности и ординарности, будем иметь:

, .

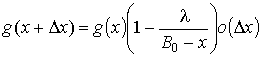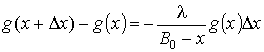Справедливо:

, ,

, .

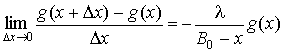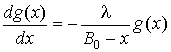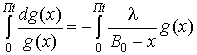Окончательно

.

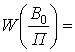Вероятность разрушения в точке x: W(t) = 1 - g(t), а функция распределения вероятности разрушения: . Коэффициент l определится из условий: , 1; p₀ – вероятность разрушения оболочки в начале процесса (x=0). Справедливо:

; .

Откуда искомый коэффициент .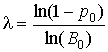

При определении количественных требований к безопасности объектов повышенного риска использовалась концепция Фармера-Расмуссена [2].

Приведенная методика использовалась при проектировании специального объекта и прошла положительную оценку при независимой экспертизе.

Литература

1. Гарькина И.А., Данилов А.М., Лапшин Э.В., Юрков Н.К. Системные методологии, идентификация систем и теории управления: промышленные и аэрокосмические приложения / Известия ВУЗов. Поволжский регион. Технические науки.–№1. –2009. –С.3-11.

2. Плющ А. А., Голованов О. А., Данилов А. М., Гарькина И. А. Обобщенная математическая модель управления безопасностью арсеналов и баз хранения боеприпасов // Вісник Хмельницького національного університету. Технiчнi науки. –№ 1. – 2007. – С. 241-246.