Сатыбалдиев О.С. –д.п.н.,
профессор
Оразбай М. - магистрант
КазНТУ
им. К.И.Сатпаева, г.Алматы, Казахстан
Применение
преобразования Лапласа для решения одномерного волнового уравнения
![]()
![]()
![]()
![]() Распространение
сейсмической волны описывается волновым уравнением. Это уравнение может быть
выведено из соотношений между напряжением, упругостью, законом Гука и законом
Ньютона.
Распространение
сейсмической волны описывается волновым уравнением. Это уравнение может быть
выведено из соотношений между напряжением, упругостью, законом Гука и законом
Ньютона.
Покажем решение начально-краевой
задачи для одномерного однородного
волнового уравнения.
Постановка задачи. Требуется найти решение уравнения
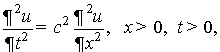 (1)
(1)
удовлетворяющее
следующим начальным и граничным условиям:
![]() (2)
(2)
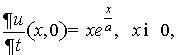 (3)
(3)
![]() (4)
(4)
![]() при
при ![]() для
для ![]() (5)
(5)
где
![]() - отклонение струны
от положения равновесия (искомая функция); из (5) следует, что в начальный
момент времени струна находится в положении равновесия; из (3) следует, что в
начальный момент времени струна имеет начальную скорость колебаний
- отклонение струны
от положения равновесия (искомая функция); из (5) следует, что в начальный
момент времени струна находится в положении равновесия; из (3) следует, что в
начальный момент времени струна имеет начальную скорость колебаний ![]() ; из (4) следует, что левый конец струны закреплен; из (5)
следует, что при удалении
; из (4) следует, что левый конец струны закреплен; из (5)
следует, что при удалении ![]() в бесконечность
отклонение
в бесконечность
отклонение ![]() стремится к нулю.
стремится к нулю.
Для построения решения задачи (1)-(5) используем
преобразования Лапласа. К обеим частям уравнения (4) применяем преобразование
Лапласа
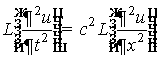 . (6)
. (6)
Известно, что
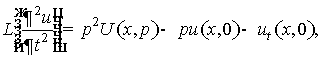 (7)
(7)
где 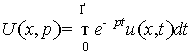 .
.
Так
как ![]() ,
, ![]() (см.(2)-(9)), то
равенство (7) перепишем в виде
(см.(2)-(9)), то
равенство (7) перепишем в виде
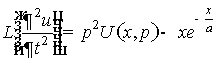 . (8)
. (8)
Рассмотрим выражение
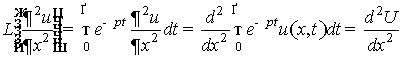 . (9)
. (9)
С учетом (7)-(9) равенство
(6) перепишем в виде
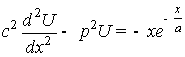 . (10)
. (10)
Характеристическое
уравнение соответствующего однородного уравнения имеет вид
![]()
При
этом общее решение соответствующего однородного уравнения имеет вид
![]()
где ![]() и
и ![]() - произвольные
постоянные.
- произвольные
постоянные.
Частное решение неоднородного
уравнения (13) будем искать в виде
![]() .
.
Если
![]() подставим в (10) и
будем приравнивать коэффициенты при
одинаковых степенях
подставим в (10) и
будем приравнивать коэффициенты при
одинаковых степенях ![]() , то получим
, то получим
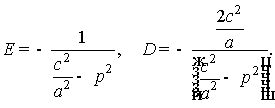
Тогда общее решение уравнения
(10) есть сумма ![]() , т.е.
, т.е.
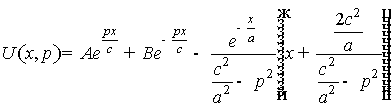 . (11)
. (11)
Если
к обеим частям (4) и (5) применим преобразование Лапласа, то получим следующие
граничные условия относительно ![]() :
:
![]()
![]() при
при ![]() .
.
Эти
условия будем использовать для нахождения значений произвольных постоянных ![]() и
и ![]() . Использование воторого условия дает
. Использование воторого условия дает ![]() , первого условия
, первого условия 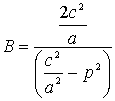 .
.
Значения ![]() и
и ![]() подставим в (11):
подставим в (11):
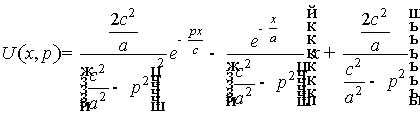
Использование формулы ![]() и соотношения
и соотношения
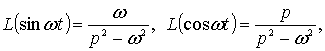
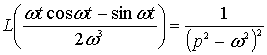
дает решение задачи (1)-(5) в виде
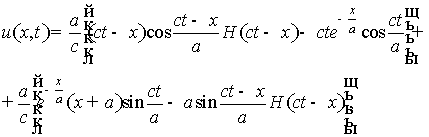
где ![]() - функция Хеввиссайда.
- функция Хеввиссайда.
Список литературы
1. Крылов А. П., Глоговский М.М., Мирчинк М.Ф.,
Николаевский Н.М., Чарный П.А. Научные основы разработки нефтяных
месторождений. – М.: РГУ нефти и газа им. И.М.Губкина, 2004. 424 с.
2. Серкеров С.А. Теория потенциала в гравиразведке и
магниторазведке. – М.: ОАО «Издательство Недра», 2000г., 350 с.