ПРИЛОЖЕНИЯ
МЕТОДОВ РАНГОВОЙ КОРРЕЛЯЦИИ
К СТАТИСТИЧЕСКОМУ
АНАЛИЗУ СВЯЗЕЙ
Карев М.Н.,
Данилов А.М.
Пензенский
государственный университет архитектуры и строительства
Рассматриваются приложения методов
ранговой корреляции к статистическому анализу связей между различными
свойствами материалов. Ранги используются при установлении связи между двумя
качественными признаками системы, когда каждый из этих признаков допускает лишь
относительное сравнение различных объектов («лучше» - «хуже») без указания
численных значений признаков [1]. Укажем три основных возможных приложений методов ранговой корреляции к статистическому
анализу связей между различными свойствами материалов (широко
использовалось при когнитивном моделировании материалов, построении
ориентированного графа и определении иерархической структуры критериев
качества).
1. Анализ
структуры совокупности упорядочений
![]() .
.
Если точки ![]() разбросаны равномерно по всей области их
возможных значений
разбросаны равномерно по всей области их
возможных значений ![]() (
(![]() ), то можно говорить об
отсутствии связи или согласованности между ранжировками. При наличии сгустка
(ядра) близко лежащих друг от друга точек можно говорить о согласованности
переменных. При наличии нескольких ядер можно говорить о наличии нескольких подмножеств
переменных с высокой степенью взаимосвязей между входящими в ядра переменными.
), то можно говорить об
отсутствии связи или согласованности между ранжировками. При наличии сгустка
(ядра) близко лежащих друг от друга точек можно говорить о согласованности
переменных. При наличии нескольких ядер можно говорить о наличии нескольких подмножеств
переменных с высокой степенью взаимосвязей между входящими в ядра переменными.
2. Анализ
интегральной (совокупной) согласованности переменных и их условная ранжировка
по степени тесноты связи каждой из них с остальными переменными. Такая
задача возникает при исследовании степени согласованности мнений группы
экспертов и условном упорядочении экспертов по их компетентности. В основе
анализа лежит определение коэффициента совокупной
согласованности - коэффициента конкордации для различных комбинаций переменных.
3. Наилучшее (в определённом смысле) восстановление
ранжировки
![]() , связанной с результирующей переменной
, связанной с результирующей переменной ![]() , по ранжировкам
, по ранжировкам ![]() , соответствующим объясняющим переменным
, соответствующим объясняющим переменным![]() (задача регрессии на
порядковых (ординальных) переменных).
(задача регрессии на
порядковых (ординальных) переменных).
Ограничимся решением первой задачи.
Теснота связи между ранжировками ![]() определяется по коэффициенту корреляции К.Спирмена
определяется по коэффициенту корреляции К.Спирмена
![]() . (1)
. (1)
Формула
(1) пригодна лишь в случае отсутствия объединённых рангов в ранжировках ![]() . В общем случае для анализа парных ранговых статистических
связей используется ранговый коэффициент корреляции Спирмена, вычисляемый по формуле
. В общем случае для анализа парных ранговых статистических
связей используется ранговый коэффициент корреляции Спирмена, вычисляемый по формуле
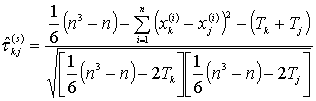 ,
, 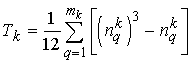 . (2)
. (2)
Здесь ранжировка осуществляется по
признаку ![]() ; имеется
; имеется ![]() групп с неразличимыми
рангами;
групп с неразличимыми
рангами; ![]() - число элементов
в q-й
группе,
- число элементов
в q-й
группе, ![]() .
.
При когнитивном моделировании эпоксидных
композитов экспериментально были
получены показатели прочности при сжатии и твердости:
|
|
Ранги |
|||||||||
|
Свойства |
Порядковый номер состава ЭК |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Прочность при сжатии, x1 |
2 |
4 |
1 |
10 |
5 |
3 |
7 |
9 |
8 |
6 |
|
Твёрдость, x2 |
2 |
5 |
1 |
10 |
4 |
3 |
7 |
9 |
8 |
6 |
Здесь объединённые ранги отсутствуют. В
соответствии с формулой (1) коэффициент ранговой корреляции Спирмена ![]() .
.
Откуда следует, возможность
ограничиться экспериментальным определением
лишь одного показателя из указанных
двух.
Устанавливалась связь между коэффициентом
структуры и коэффициентом энергоёмкости ЭК.
|
|
Ранги |
|||||||||
|
Показатели |
Порядковый номер состава ЭК |
|||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Коэффициент структуры, x13 |
10 |
4 |
5,5 |
9 |
8 |
7 |
5,5 |
3 |
2 |
1 |
|
Коэффициент энергоемкости, x14 |
10 |
3 |
2 |
6,5 |
6,5 |
9 |
4 |
5 |
8 |
1 |
Здесь при ранжировке по признаку x13 имеется одна группа с
неразличимыми рангами 5,5; число элементов в группе m13 = 1. Имеем: ![]() . Аналогично для x14:
T14 = 0,5.
Имеем:
. Аналогично для x14:
T14 = 0,5.
Имеем: ![]() .
.
Отсюда следует, что коэффициенты структуры и энергоёмкости должны определяться по
экспериментальным данным самостоятельно.
При анализе парных ранговых статистических
связей между ранжировками часто используется и ранговый коэффициент корреляции Кендалла.
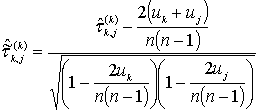 ;
; 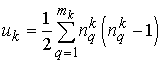 ,
, 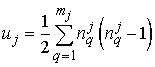 .
.
Коэффициенты ранговой корреляции Спирмена и Кендалла связаны между собой (оба коэффициента - линейные функции от числа инверсий в перестановке). При определении коэффициентов Спирмена и Кендалла речь, таким образом, идет о выборочных характеристиках ранговой связи.
Литература
1.
Гарькина И.А., Данилов
А.М. Управление в сложных технических системах: методологические принципы
проектирования / Региональная архитектура и строительство. № 1. 2012. – C. 39-42.