К.т.н. Куимова Е.И., к.п.н. Ячинова С.Н.

Пензенский государственный университет архитектуры и строительства, Россия

К вопросу изучения дифференциальных уравнений

Многие студенты рассматривают изучение математики как дисциплину, предназначенную для их общего развития, совершенно не осознавая ее практическую значимость. Это связано с отсутствием или недостаточным количеством профессионально ориентированных задач. При изучении дифференциальных уравнений студентам старших курсов, магистрантам, обучающимся по направлению «Строительство» необходимо разъяснять не только методы их решения, но и их применение при моделировании технологических процессов и обработки результатов экспериментов.

процедуру идентификации кинетических процессов формирования основных физико-механических характеристик строительных материалов можно показать на простых примерах. Обобщенная динамическая модель кинетических процессов является решением задачи Коши:

,

где определяются видом исследуемого кинетического процесса.

Рассмотрим результаты исследования прочности лакокрасочных покрытий на пористой цементной подложке.

Как показывает опыт, нельзя утверждать, что на разных этапах активной стадии накопления повреждений интенсивность изменения свойств покрытия одинакова, на графиках может наблюдаться несколько точек перегиба. В зависимости от вида покрытия и некоторых других причин первая половина активной стадии (средняя доля всей долговечности покрытия) характеризуется особенно резким увеличением всех негативных параметров, в дальнейшем процессы протекают более плавно. Опишем кинетику разрушения покрытий дифференциальными уравнениями порядка выше второго. Это означает, что при анализе процесса необходимо учитывать не только скорость изменения контролируемого параметра, но и как минимум ускорение. Рассматриваем в качестве модели процесса разрушения функцию , являющуюся решением дифференциального уравнения третьего порядка. Коэффициенты характеризуют скорость изменения контролируемого параметра на разных этапах старения покрытия.

Анализируя эмпирические кривые по кинетике накопления повреждений, можно принять, что (для площади поверхности покрытия характерно даже ), .

В качестве примера рассмотрим изменение площади поверхности поливинилацетатцементного покрытия в процессе увлажнения.

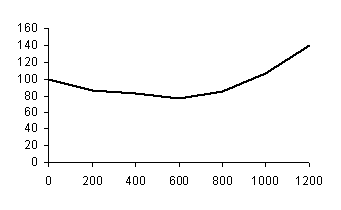
Рис.1. Изменение площади поверхности ПВАЦ покрытия в процессе старения

Из экспериментальных данных следует: , ,, .

Для идентификации параметров модели решаем систему уравнений

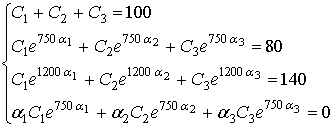
Из первых трех уравнений получим

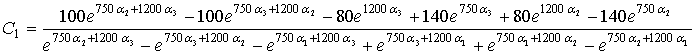
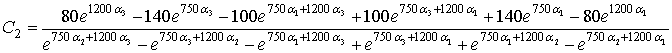
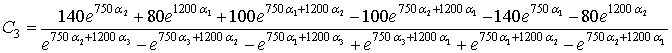Определим и по экспериментальной характеристике Y(t) (рис. 1). Так как , то составляющая определяет процесс до конца инкубационного периода, т. е. при . Значение можно определить по концу экспериментально полученного процесса Y(t). А именно,

, при , , при ,

, .

В данном случае, , .

Из четвертого уравнения системы получим неявное выражение для

.

Приближенное решение этого уравнения даст .

В результате решение исходного дифференциального уравнения представится в виде .

Из изложенного выше вытекает следующий алгоритм идентификации кинетических процессов данного вида:

1) По начальным изменениям инкубационного периода определяется , по концу эмпирической кривой – ;

2) Константы С₁, С₂, С₃ представляются как функции от ;

3) По характерной точке эмпирической кривой строится уравнение (3), находится приближенное значение константы ;

4) Наконец, определяется

.

Предложенный алгоритм может быть использован при решении других задач строительного материаловедения с возможностью описания рассматриваемых процессов как решений дифференциальных уравнений третьего порядка.