К. п. н. Быкова Т.П.

ФГБОУ ВПО «Борисоглебский государственный педагогический институт». Россия.

Комплексные математические задания как средство достижения планируемых результатов освоения основной образовательной программы начального общего образования

Великий русский математик Н.И. Лобачевский, говорил, что математика – это наука, которая ум в порядок приводит. Воспитывать культуру мышления – вот, пожалуй, одно из главнейших предназначений математического образования. Математика призвана сформировать такие качества мышления, как логичность, строгость, четкость, последовательность, умение выполнять такие мыслительные операции, как анализ, синтез, обобщение, классификация и т.д., умение выбирать наиболее рациональные пути решения стоящей задачи, умение оперировать с понятиями и др., входящие в представление о мыслительной культуре. Еще одна важнейшая задача обучения математике - сформировать способность полноценно и аргументировано обосновывать свои выводы и действия, оперируя известными теоретическими положениями, логически правильно выстраивать свои рассуждения, доказательно и последовательно излагать свои мысли.

Все эти задачи, издавна стоящие перед математическим образованием, особенно актуальны в настоящее время, когда Российская школа переходит на обучение по новым Федеральным государственным образовательным стандартам.

Стандарт устанавливает требования к результатам обучающихся, освоивших основную образовательную программу начального общего образования: личностным, метапредметным и предметным.

С переходом на обучение по новым стандартам содержание начального математического образования практически не изменилось. Возникает вопрос, за счет чего же будут достигаться результаты обучения, сформулированные в новом Федеральном стандарте? Ответ на этот вопрос очевиден: за счет специально подобранной для каждой темы системы упражнений.

Подбирая задания как для работы в классе, так и для организации домашней работы школьников, учитель должен четко понимать на достижение каких результатов работает то или иное упражнение. Желательно включать в урок такие задания, которые будут способствовать достижению целого комплекса результатов: предметных, метапредметных, личностных. И здесь ограничиваться только заданиями, имеющимися в учебниках, было бы неправильным.

Приведем пример такого комплексного задания для 4 класса. Эта задача может быть предложена при изучении темы «Числа от 1 до 1000. Арифметические действия».

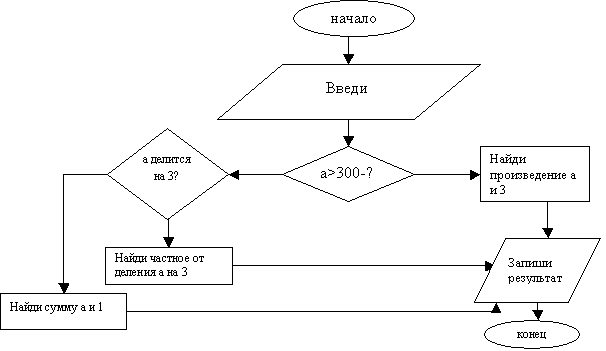
Задача: «Вычислительная машина выполняет следующую программу:

нет да нет

да

Найди результат выполнения этой программы при а=157; а=342; а=529. Подумай, сколько цифр будет содержать число, являющееся результатом выполнения этой программы при других значениях а. Зависит ли это от того, чему равно а? Измени данную программу так, чтобы результатом её выполнения всегда было двузначное число».

Можно утверждать, что результат выполнения данной программы будет трёхзначным числом при всех возможных значениях а. Действительно, в качестве а, согласно программе, вводится трёхзначное число, то есть возможное минимальное значение а – это 100. Если а не больше 300, то его умножают на 3. Возможное минимальное значение при этом будет 300 (100·3=300). Наибольшее число, не большее 300 – это 300. 300 · 3 = 900 – трёхзначное число. То есть если а не больше 300, то результат не меньше 300 и не больше 900, следовательно, результат - трёхзначное число.

Рассмотрим случай, когда а > 300. При этом возможны 2 варианта:

1) а делится на 3. В этом случае результат– это частное а и 3. 300 : 3 = 100 – трёхзначное число. Если же делимое будет больше 300, то частное будет больше 100, то есть будет трёхзначным числом. При этом при делении трехзначного числа на 3 не может получиться число, записанное более чем тремя знаками. Поэтому результат выполнения алгоритма при а> 300 и при а, делящемся на 3, всегда трехзначное число.

2) а не делится на 3. Тогда результат это значение суммы а+1. Так как а – трёхзначное число, то а+1 тоже трёхзначное число, за исключением случая, когда а=999. 999+1 = 1000 – четырёхзначное число. Но 999 делится на 3 (999 : 3=333).

Итак, при любом возможном значении а результат - трёхзначное число. Чтобы в результате всегда получалось двузначное число, программу можно изменить так: в блоке ввода данных заменить требование «введи трёхзначное число» на требование: «введи двузначное число». В первом блоке проверки условия (логическом блоке) заменить условие «а > 300» на условие «а > 30». Остальную программу оставить без изменений.

Задание направлено на развитие алгоритмического мышления младших школьников, формирование умения действовать с алгоритмом – это предметный результат предметной области «Математика и информатика». Выполняя задание, дети учатся не только находить результат выполнения алгоритма, но и исправлять алгоритм таким образом, чтобы результат всегда удовлетворял указанным требованиям. А это работа, направленная на формирование умения планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей, то есть на формирование регулятивного УУД, входящего в группу метапредметных результатов. Кроме того, работа над заданием включает выполнение рассуждений, требующих достаточно серьёзного анализа ситуации, построения дедуктивных и индуктивных умозаключений. Все это относится к логическим УУД, также входящим в группу метапредметных результатов. Работа над заданием способствует развитию математической речи, формированию умения выдвигать и проверять гипотезы, аргументировано обосновывать свои выводы. Эти умения относятся к коммуникативным УУД. Выполнение задания способствует совершенствованию вычислительных навыков, что входит в предметные результаты обучения математики, а также повторению приёмов умножения и деления трёхзначного числа на однозначное, то есть решению текущих задач изучения данной темы.

Литература:

1. Быкова Т.П. Нестандартные задачи по математике. 4 класс. – М.: Экзамен, 2010