Влияние температуры на проводимость композитного полимерного материала, содержащего углеродный наполнитель.

Н.Н.Комова*, В.М.Капитонов*, И.И.Барашкова**, В.А.Марков*
*Московский государственный университет тонких химических технологий им. М.В.Ломоносова
** Институт химической физики им. Н.Н.Семёнова РАН

Полимерные композиционные материалы, содержащие технических углерод, обладают достаточно заметной электропроводностью и могут быть использованы при изготовлении терморегулирующих нагревательных элементов [1, 2]. Эксплуатация таких элементов сопряжена с изменением температуры в широком диапазоне. В связи с этим необходимо знание зависимости электропроводности или сопротивления от температуры материала.
Известно, что механизм электропроводности подобных композиционных материалов имеет сложный характер. Этот характер обусловлен свойствами поверхности технического углерода, что оказывает влияние на электропроводность композита через его структурность. Из-за сложной структуры частиц технического углерода теоретический расчёт электропроводности композита с данной концентрацией наполнителя оказывается трудной задачей. Для объяснения поведения композитов существуют две теории, с помощью которых удаётся в той или иной степени описать наблюдаемые закономерности.
Согласно первой теории, справедливой для систем с низкой электропроводностью, проводимость определяется процессом эмиссии электронов, скорее всего туннельным переносом между частицами, расстояние между которыми менее 5 нм [3].
По второй теории, для случая высокой электропроводности, подразумевается, что контакты между частицами являются омическими и рассчитывается вероятность образования проводящих цепочек. В этой теории основное внимание уделено геометрическому фактору, связывающему величину электропроводности со случайным набором проводящих цепочек. Теория определяет отношение электропроводностей композита σ и проводящего компонента σ_с как произведение отношения доли проводящих и непроводящих элементов и вероятности образования цепочки (р) и геометрического фактора - площади поперечного сечения проводящего элемента (С): σ/σ_с=f_υ·p·C² [4]. Такой подход к анализу проводимости композиционных материалов аналогичен описанию систем с позиции фрак-тальной физики [5].
С позиций разработанных теорий может быть рассмотрено изменение сопротивления композита с ростом температуры. Влияние нагревания на электрические свойства полимерных композиционных материалов имеет сложный характер. У электропро-водящих полимерных композитов могут наблюдаться значительные изменения электрического сопротивления, характеризуемые как положительными, так и отрицательными температур-ными коэффициентами [1,6,7]. В низкотемпературных интервалах (25-275 K) наблюдается экспоненциальное падение электрического сопротивления, характерное для полупроводниковых материалов [8].

При более высоких температурах обычно наблюдается рост электрического сопротивления, который связывают с увеличением теплового расширения полимера [9]. Изменение электрического сопротивления при повышении температуры объясняют увеличением расстояний между частицам [10]. При анализе исследуемых зависимостей сопротивления композита от температуры следует учитывать наличие кристаллической фазы в полимерной матрице, что делает механизм изменения электрического сопро-тивления более сложным. В результате у электропроводящих композиционных материалов на основе кристаллизующихся полимеров при температурах, близких к температурам плавления, обнаруживается резкий рост электрического сопротивления [11]. В целом из-за сложного строения таких композиционных материалов вопрос о причинах резкого повышения и падения электрического сопротивления остается открытым [12]. В настоящей работе предпринята попытка установить причины возникновения экстремальной зависимости сопротивления от температуры для композиционного материала на основе полиэтилена и технического углерода.

Объектами исследования являлись композиции на основе термопластичных полимеров: полиэтилена высокой плотности ПЭВП 277-73 (ГОСТ 16338-85), с содержанием электропроводящего технического углерода УМ-76 (ТУ 38-10001-94) – 11,7 об % (около 20 масс %).Вводимое количество наполнителя рассчитывалось таким образом, чтобы его значение позволило превысить порог пропускания (перкаляционный барьер) [13].

Композиции приготовляли в закрытом роторном смесителе «Брабендер» с объемом рабочей камеры 30 мл с жидкостным обогревом в течение 10 мин со скоростью вращения роторов 50 об/мин. Температуры смешения составила для ПЭНП – 140 °C. Изготовление образцов проводилось на гидравлическом прессе с обогреваемыми стальными плитами при температуре 200 °C в течение 5 мин. Процесс прессования проходил в два этапа. Предварительно изготавливались пластины, а затем на втором этапе в них впрессовывались контакты. Отпрессованные образцы охлаждали между стальными плитами пресс-формы в течение 20 мин с 200 °C до 70 °C, окончательное остывание

проводили после изъятия образцов на воздухе. Для формирования контактов использовалась латунная сетка Л-80 (ГОСТ 6613-86), которую перед использованием обезжиривали и зачищали наждачной бумагой. Размеры образцов – 40x5x1 мм, расстояние между контактами – 30 мм.

Измерение удельного объемного электрического сопротивления образцов (ρ) при повышенных температурах (Т) проводилось в термокамере, обеспечивающей скорость нагрева 10 °C/мин. Электрическое сопротивление образцов измеряли омметром DT9208A при напряжении 9 В. С целью исследования влияния температур изотермической кристаллизации на изменение электрического сопротивления часть образцов с подключенными к омметру контактами после формования при 200 °C быстро (за время не более 1 с) изымались из пресса и помещались в термостат с жидким полидиметилсилоксаном (ПМС-200), предварительно разогретый до заданной температуры от 23 до 120 °C. В этой жидкости они изотермически кристаллизовались в течение 5 мин. При этом проводилось непрерывная фиксация изменяющегося электрического сопротивления. Большой объем термостатирующей жидкости и ее интенсивное перемешивание позволяют считать ее температуру в ходе эксперимента постоянной. Окончательное охлаждение образцов проводилось после их изъятия из термостата на воздухе.

Процесс плавления (стеклования для УПС) электропроводящих образцов исследовали методом ДСК на приборе ТА Pyris 6 DSC Perkin Elmer при нагреве от 25 до 250 °C со скоростью 10 °C/мин (как и при исследовании изменения электрического сопротивления при нагревании).

Степень кристалличности рассчитывали, используя уравнение: α_кр=ΔН_пл/ ΔН_пл⁰ 100%, гдеΔ Hпл. – энтальпия плавления полимерной фазы образца, рассчитанная по кривой ДСК с учетом массовой доли технического углерода, ΔН_пл⁰– энтальпия плавления полимера со 100%-ой кристалличностью [14].

На рис. 1 представлены результаты измерений электрического сопротивле-ния при нагревании электропроводящей полимерной композиции, изготов-ленной на основе ПЭНП. Экспериментальные данные представлены в виде относительного изменения удельного электрического сопротивления при ρ_Т/ρ₂₀, где ρ_Т - удельное электрическое сопротивление при температуре Т. У всех исследованных образцов эти зависимости имеют четкий экстремум (пик) электрического сопротивления в температурных областях плавления полимерной матрицы.

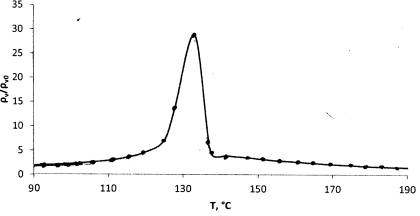
Рис. 1. Зависимости относительного электрического сопротивления ρ/ρ0 от температуры T для композиции на основе ПЭНП, содержащей 20мас.% технического углерода.
Зависимости на рис.1 можно разделить на две области: до 132^оС относительное удельное сопротивление образцов увеличивается (энергия активации этого процесса составляет Е_1ρ= 27,4 кДж/моль), при температуре выше 132 ^оС относительное удельное сопротивление образцов падает (энергия активации этого процесса Е_2ρ=-32,31 кДж/моль).

На рис. 2 приведены спектры ДСК (дифференциальной сканирующей калориметрии) для случая нагрева (а) и охлаждения (б). Максимумы спектров сдвинуты по оси температур на 15^о, что может указывать на релаксационный процесс в системе.
Сравнивая рис.1 и рис.2 а, можно отметить, что экстремальные значения зависимости на них принимают при значениях температур, расположенных довольно близко:130 и 132^о С.Это даёт основание предположить, что обе зависимости отражают один и тот же процесс.
Расчёт изменения степени кристалличности композита с использованием рисунка 1а позволяет определить изменение этой величины в процессе проплавления материала. Результаты зависимости степени кристалличности от температуры представлены на рис.3. Энергия активации процесса уменьшения степени кристалличности равна 4,3 кДж/моль.По своему смыслу эта величина представляет энергию активации проплавления материала. Как видно из представленных зависимостей проплавление материала уменьшает степень кристалличности до нулевого значения, но при этом увеличивается относительное удельное сопротивление. Однако, предположить, что обе зависимости отражают один и тот же процесс не вполне корректно, поскольку их энергии активации различаются в 6 раз. Поэтому следует принять во внимание тот факт, что наряду с процессом увеличивающим сопротивление системы с увеличением температуры развивается процесс уменьшения сопротивления. Разница энергий этих двух процессов составляет 4,9 кДж. Эта величина близка к значению энергии активации уменьшения степени кристалличности.
Анализ полученных зависимостей даёт основания предположить следующий механизм реализации проводимости исследуемой композиции. С увеличением температуры происходит увеличение флуктуационных процессов в образовавшихся цепочках конгломератов из частиц технического углерода, являющихся токопроводящими каналами. В результате контактные связи могут претерпевать локальный разрыв, что приведет к увеличению сопротивления. Этому процессу также будет способствовать процесс уменьшения кристаллической фазы, т.е. разупорядочение системы и её деструктуризация. Однако, необходимо также учитывать и процесс увеличения подвижности носителей зарядов с увеличением температуры.

Кроме того, процесс деструктуризации при проплавлении полимерной матрицы приводит к изменению фрактальной размерности системы, что проявится в свойствах системы. Согласно представлением фрактальной физики существует критическое значение фрактальной размерности, при приближении к которой система теряет устойчивость и переходит в нестабильное состояние, при этом параметры либо быстро возрастают, либо быстро убывают. Так, при размерности D больше 1,6 система неустойчива и переходит в новое состояние. Процесс изменения степени кристалличности в полной мере можно отнести к фрактальному явлению. Исследования зависимостей степени кристалличности и относительного удельного сопротивления системы дают аналитическое выражение следующего вида:
(ρ/ρ₀)^2,56=А-Bα,

где A и B представляют величины, зависящие от природы полимерной матрицы и наполнителя, поверхности наполнителя, его концентрации и т. п.

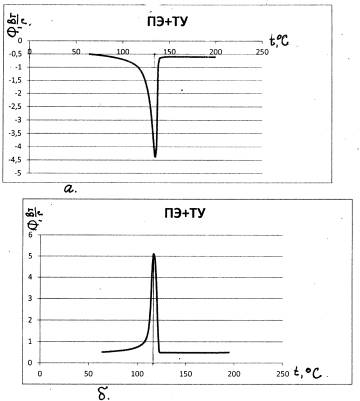
Рис.2.Спектры ДСК ПЭНП, наполненного 20 мас. % технического углерода.
а - процесс нагревания; б- процесс охлаждения.

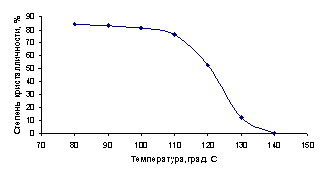
Рис.3. Изменение степени кристалличности композита ПЭНП с 20
мас.% ТУ с увеличением температуры.
А величина степени есть по своему смыслу фрактальная размерность. Поскольку она превышает критическое значение, то в процессе проплавления система переходит в новое состояние. В этом состоянии частицы техничес-кого углерода занимают новое упорядоченное положение, определенное новой фрактальной размерностью, и проводимость возрастает до прежних размеров.
Литература

1. Zhang W., Dehghani-Sanij A. A., Blackburn. R. S. Carbon based conductive polymer composites // J. Mater. Sci. 2007. Vol. 42. P. 3408-3418.

2. Xiao A. Y., Tong Q. K., Savoca A. C., Van Oosten H. Conductive ink for through hole application// IEEE Trans. Compon. Pack. Technol. 2001. Vol. 24. P. 445-449.

3. Sommers. D. J. Carbon black for electrically conductive Plastics // Polym. Plast. Technol. Eng.1984. Vol. 23(1). P. 83-98.
4. Mukherjee A.K. and Party M. Electrical Properties of CAPP fnd PVC-DOP-CAPP System// J. jf Applied Polymer Scienct/V/39/1990/P/1485-1493
5.Карпов С.В., Герасимов В.С., Исаев И.Л., Обущенко А.В. Моделирование роста агрегатов наночастиц, воспроизводящее их естественную структуру в дисперсных системах//Коллоидный журнал.Т.68.№4. 2006.С.484-494

6. Heaney M. B. Resistance-expansion-temperature behavior of a disordered conductor-insulator composite // Appl. Phys. Lett. 1996. Vol. 69. P. 2602-2604.

7. Hindermann-Bischoff M., Ehrburger-Dolle F. Electrical conductivity of carbon blackpolyethylene composites. Experimental evidence of the change of cluster connectivity in the PTC effect // Carbon. Vol. 2001. 39. P. 375-382.

8. Tawalbeh T. M., Saq’an S., Yasin S. F., Zihlif A. M., Ragosta G. Low temperature electrical conductivity of low-density polyethylene/carbon black composites // J. Mater. Sci.: Materials In Electronics. 2005. Vol. 16. P. 351-354.

9. Tang H., Chen X., Tang A., Luo Y. Studies on the Electrical Conductivity of Carbon Black Filled Polymers // J. Appl. Polym. Sci. 1996. Vol. 59. P. 383-387.

10. Dafu W., Tiejun Z., Yi X.-S. Resistivity-Volume Expansion Characteristics of Carbon Black-Loaded Polyethylene // J. Appl. Polym. Sci. 2000. Vol. 77. P. 53-58.

11. Beaucage G., Rane S., Schaefer D. W., Long G., Fischer D. Morphology of Polyethylene–CarbonBlack Composites // J. Polym. Sci.: Part B: Polym. Phys. 1999. Vol. 37. P. 1105-1119.

12. Dai K., Zhang Y.-C., Tang J.-H., Ji X., Li Z.-M. Anomalous Attenuation and Structural Origin of Positive Temperature Coefficient (PTC) Effect in a Carbon Black (CB)/Poly(ethylene terephthalate) (PET)/Polyethylene (PE) Electrically Conductive Microfibrillar Polymer Composite with a Preferential CB Distribution //J. Appl. Polym. Sci. 2012.Vol. 125. P. E561-E570.

13.Э.Р. Блайт,Д. Блур. Электрически свойства полимеров.М.Физматлит.2008. 373 с.
14. Yin C.-L., Liu Z.-Y., Gao Y.-J., Yang. M.-B. Effect of compounding procedure on morphology and crystallization behavior of isotactic polypropylene/high-density polyethylene/carbon black ternary composites // Polym. Adv. Technol. 2012. Vol. 23. P. 1112-1120.