Моделирование процесса распространения органических примесей в открытых каналах

 

 

А.И. Есин

М.П. Горбачева

ФГБОУ «Саратовский ГАУ» им. Н.И. Вавилова, г. Саратов (Россия)

Постановка проблемы.  Процесс распространения «мусора» растительного происхождения в водоемах очень актуален в настоящее время. Однако данный процесс изучен очень мало, особенно  движение потока воды в открытом  канале, в котором происходят биологические процессы, сопровождающиеся распространением примесей растительного происхождения (зеленые водоросли, плавающие растительные останки, другие взвешенные наносы, способные к естественному увеличению своей массы).

Анализ исследований и публикации.  Разработана методика теоретического исследования по математической модели процесса распространения органических примесей в канале и проведены вычислительные эксперименты на ЭВМ.

Целью публикации является научное обоснование развития процесса загрязнения оросительной воды мусором растительного происхождения с помощью математической модели.

Основные результаты исследования.  На основе двумерного в плане подхода получена математическая модель процесса. Сформулирована и решена краевая задача. Исследованы частные случаи решения.

Рассмотрим установившееся движение осредненного турбулентного потока воды в открытом русле. Согласно [1] процесс распространения в воде различных примесей (зеленые водоросли, плавающие растительные останки, шуга и т.п.)  в двумерной плановой постановке описывается уравнением диффузии:

 

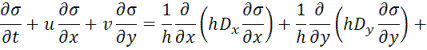
,                                          (1)

где   σ – осредненное значение концентрации примеси на вертикали;  t – время;  x, y – прямоугольные координаты;  u, v – средние по глубине значения плановых проекций скорости на оси координат; h – местная глубина потока; Dx − суммарный продольный коэффициент диффузии, учитывающий турбулентную и конвективную диффузию;  Dy – суммарный поперечный коэффициент диффузии, включающий коэффициент конвективной диффузии D0  за счёт поперечной  циркуляции; GH , GZ   − поток примеси через свободную поверхность и дно русла, соответственно; σH , σZ − концентрация примеси на свободной поверхности и дне русла, соответственно; W − гидравлическая крупность примеси;   fист – мощность источников порождения примеси в единице объема жидкости за счет химических или биологических процессов.

Если ввести обозначения:

         ;   

то уравнение (1) примет вид:

                                     (2)                             

В естественных координатах s, ψ [1] для уравнения (2) имеем:

                                                  (3)

где w – модуль вектора скорости в произвольной точке плана течения; ψ = const – семейство линий тока; s = const – семейство ортогональных  им линий: q – вспомогательная функция, удовлетворяющая уравнению

,                                                             (4)

где q - угол наклона вектора скорости  к продольной оси х.

 Рассмотрим класс движений воды в канале, характеризующийся условием q » 0, т.е. когда  кривизной потока в плане можно пренебречь. В этом случае из уравнения (4) следует, что  q – произвольная функция от s, которую для простоты положим равной единице.

Тогда уравнение (3)  можно переписать как:

.                                         (5)

Далее будем считать движение  воды равномерным: h=h(y), w=w(y). Согласно исследованиям Элдера [2], Саффмена [3],   Караушева А.В. [4] эффективный коэффициент продольной диффузии Ds в равномерном открытом потоке определяется по формуле

Ds= AhU*,                                                                         (6)

где А − безразмерный эмпирический коэффициент;    − динамическая скорость потока; С – коэффициент Шези; V – средняя скорость течения.

Многочисленные  эксперименты,  проведённые Элдером  [2], Фишером [5] и другими исследователями показывают, при логарифмическом профиле скорости, наиболее часто реализующемся на практике, эмпирический коэффициент А принимает следующие значения: 6,1≤ A ≤ 25.

         Из  (6)  следует, что при равномерном движении воды Ds не зависит от s. Поэтому далее для упрощения записи полагаем Ds = D.

Для многих прикладных задач можно считать [1], что при равномерном движении эффективный коэффициент поперечной диффузии Dy не зависит от у, тогда:

                                             (7)

Положив  h = hmax= h0 – глубине равномерного движения, аппроксимируем зависимость (7) следующей зависимостью:

 .                                                    (8)

         С учётом  сделанных предположений уравнение диффузии (5) принимает вид:

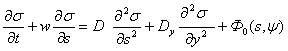                    .                                 (9)

           Следуя [1], проведем осреднение уравнения (9) по живому сечению потока:

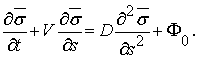                                                (10)

где 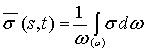      –    среднее значение концентрации примеси в живом сечении потока.                          

Уравнение (10) известно как дифференциальное уравнение Эйнштейна-Колмогорова для функции вероятности  [6]. Для отыскания единственного решения уравнения (10) необходимо задать начальные и граничные условия. Как правило, мелиоративные каналы (магистральные, распределительные, оросительные) можно считать относительно длинными (h/L << 1). В задачах подобного типа обычно считают, что канал полубесконечен, а продольная координата изменяется в пределах 0 ≤ s ≤ ∞.

Таким образом, краевая задача для полубесконечного канала состоит в отыскании решения уравнения (10) в области 0 ≤ s ≤ ∞; t ≥ 0, удовлетворяющего условиям:

                                                               (11)

                                                                (12)

где – заданные функции.

Для того чтобы условия (11), (12) определяли единственное решение задачи, необходимо выполнение условия ограниченности концентрации примеси в бесконечности (при s → ∞):

при 0 ≤ s < ∞, t ≥ 0,                                             (13)

где М > 0 – некоторая постоянная.

Во многих случаях скорость движения воды в мелиоративных каналах, как магистральных, распределительных, так и оросительных является относительно малой величиной  (V << 1). Это объясняется в первую очередь резким сокращением   количества работающих дождевальных машин.   Тем не менее, даже при минимальном количестве работающих дождевальных машин магистральные и распределительные каналы должны быть  наполнены до необходимых отметок. Малые скорости течения являются одной из причин размножения синих водорослей («цветения» воды).

Поэтому будем считать далее среднюю скорость движения воды V в канале малым параметром. Следуя общепринятой методике решения задач о малых возмущениях [1, 7], найдем решение задачи (10) – (13) в виде асимптотического разложения по малому параметру V:

                                                  (14)

Решение краевой задачи в нулевом приближении имеет вид [1, 7]:

                                               (15)

где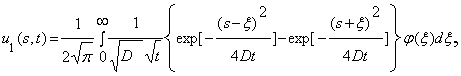                 

                      

                        ,                                

.

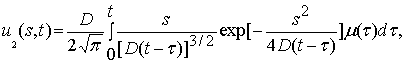
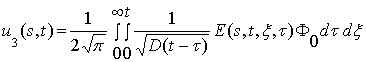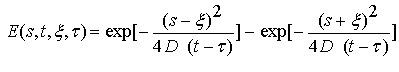Последующие приближения представим в виде рекуррентного соотношения:

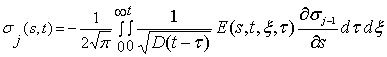,   j = 1, 2, …  .       (16)

Ограничимся рассмотрением   частного случая решения (15) для практически важных течений, встречающихся при эксплуатации гидромелиоративных каналов. Концентрация примеси в канале в начальный момент времени и в начальном створе постоянны: ; .

При этом относительно функции Ф0(s,ψ)  будем предполагать, что мощность источников порождения примеси в ходе биологических процессов постоянна  Ф0 = f0 = const.

В этом случае решение имеет вид:

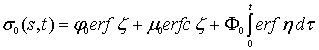,                                        (17)

где 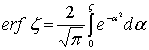 – интеграл вероятности (интеграл ошибок),        .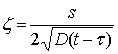

Используя разложение функции erf z в степенной и асимптотический

ряды [1, 7] и взяв главные члены разложений, из решения (17) находим:

,                                   (18)

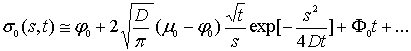
,               (19)

С учетом (18), (19),  из (16) получаем:   σ1 (s, t) ≈ 0,       следовательно,

                       σ(s, t) @  σ0 (s, t) + O(V  2).                                                 (20)

По решению (20) проведены вычислительные эксперименты при различных значениях параметров потока, результаты которых представлены на рис. 1, 2.

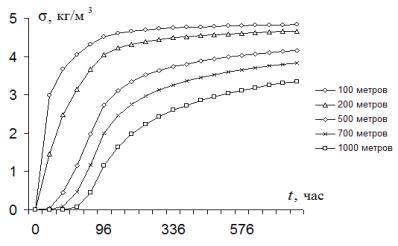
Рисунок 1 – Изменение концентрации примеси по  створам при

µ0 = 5 кг/м3, D = 1 м2/с

 

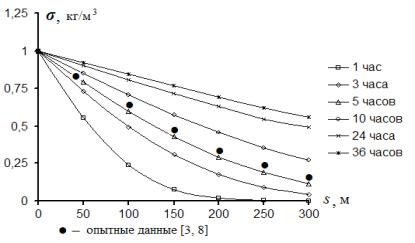
Рисунок 2 – Изменение концентрации примеси вдоль канала при

µ0 = 1 кг/м3, D = 1 м2/с

 

На рис. 2 представлены также опытные данные Элдера [2] и Фишера [5], свидетельствующие о достаточно хорошем совпадении расчетных и натурных результатов.

 

 

ЛИТЕРАТУРА

1.       Есин,  А.И.  Численная гидравлика (монография) / А.И. Есин. − Саратов: Изд. ФГОУ ВПО «Саратовский ГАУ», 2013. −160 с.

2.       Elder, J.W. The dispersion of marked fluid in turbulent shear flow /J.W. Elder // “J. Fluid Mech.”, 1959, № 4. P. 544-560.

3.       Saffman, P.G. The effect of wind shear on horizontal spread from an instanteneous ground source /P.G. Saffman // «Quarterly Journ. of the Roy. Meteorol. Soc.», London, 1962, vol. 88. p. 19-23.

4.       Караушев,  А.В. Проблемы динамики естественных водных потоков / А.В. Караушев. –  Л.: Гидрометеоиздат, 1960. 396 с.

5.       Fischer, H.B. Longitudional dispersion and turbulent mixing in open channel flow / H.B. Fischer // “Ann. Rev. Fluid Mech.”, 1973, vol. 5. P. 59 – 78.

6.       Тихонов  А.Н., Самарский  А.А. Уравнения математической физики / А.Н. Тихонов, А.А. Самарский. –  М.: Наука, 1972. 736 с.

7.        Есин А.И. Диффузионная модель распростоанения примесей органического происхождения в мелиоративных каналах/ А.И. Есин, М.П. Горбаачева // Вестник Саратовского Госагроуниверситета. №2, 2008. С.40-41.