Технические науки/11.Робототехника
Бергер Е.Э.
Херсонский национальный
технический университет
ПРОЕКТИРОВАНИЕ
НАПРАВЛЯЮЩИХ МЕХАНИЗМОВ
Рассмотрим проектирование механизмов и
методику расчета параметров их настройки на воспроизведение заданных кривых
2-го порядка.
|
|
(1) |
|
|
(1`) |
 Для упрощения формул настройки принимаем
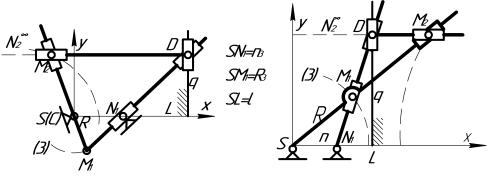
Для упрощения формул настройки принимаем ![]() , т.е. соответственные точки N1, N2
определяем на луче SN1N2, перпендикулярном
оси гомологии q (рис.1). При удалении точки N2 в бесконечность (
, т.е. соответственные точки N1, N2
определяем на луче SN1N2, перпендикулярном
оси гомологии q (рис.1). При удалении точки N2 в бесконечность (![]() )точка (М2) определяется пересечением луча SМ1М2 с прямой
)точка (М2) определяется пересечением луча SМ1М2 с прямой ![]() , параллельной оси SX (показано
на рис. 1 пунктиром).
, параллельной оси SX (показано
на рис. 1 пунктиром).
При этом формулы (1) упрощаются к виду
|
Рис.1 |
(2) |
|
|
(2`) |
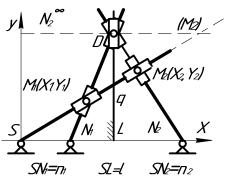
Совмещая кривошип SM1 с кулисой SM1M2, а его
шарнир С с шарниром S,получаем две модификации
коникографов, показанные на рис.2. При перемещении точки М1 по окружности
точка М2 описывает кривые 2-го порядка с фокусом в точке S. Их уравнение определяется подстановкой выражений (2)
в уравнение (3) (индексы 2 при х, у опущены).
![]() (3)
(3)
|
|
|
Рис.
2
|
|
(4) |
Уравнение (4) выражает эллипс при R<n, гиперболу при
R>n и параболу при
R=n. В каноническом
виде уравнение (4) записывается в форме
|
|
(5) |
где полуоси ![]() ,
, ![]() , фокусное расстояние
, фокусное расстояние ![]() ; Отсюда определяются параметры воспроизводимых кривых.
; Отсюда определяются параметры воспроизводимых кривых.
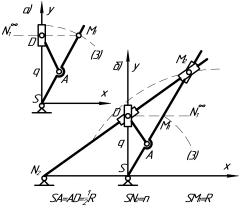
При совмещении направляющей q с осью ординат получаем коникограф, изображенный на
рис.3. Пишущий штифт М2
воспроизводит кривые 2-го порядка вида (5), где ![]() ,
, ![]() ,
, ![]() (6)
(6)
Это кривая с фокусом в точке S является эллипсом при R<n, гиперболой
при R>n и параболой
при R=n.
|
|
|
Рис. 3
Рис.
4
При задании кривых полуосями a и b
параметры настройки механизма определяются по формулам ![]() ; для параболы
; для параболы ![]() (7)
(7)
Если удалить в бесконечность точку N1, то
точка Dна оси q будет определяться пересечением луча ![]() параллельного SN2X (рис.4. а). При
перемещении М1 по окружности (3)
параллельного SN2X (рис.4. а). При
перемещении М1 по окружности (3) ![]() построение точки D может выполняться
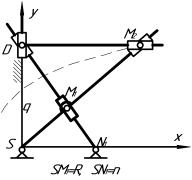
кривошипно-ползунным механизмом SAD, в котором SA=AD=1/2R.Точка М2 определяется пересечением кулис SM1M2 и N2DM2 (рис. 4б).
Формулы преобразования (соотношение координат
точек М1 и М2) имеют вид
построение точки D может выполняться
кривошипно-ползунным механизмом SAD, в котором SA=AD=1/2R.Точка М2 определяется пересечением кулис SM1M2 и N2DM2 (рис. 4б).
Формулы преобразования (соотношение координат
точек М1 и М2) имеют вид ![]() ;
; ![]() (8)
(8)
![]() ;
; ![]() (8`)
(8`)
При перемещении M1 по
окружности (3) точка М2 описывает конические сечения с фокусом S.
![]() (9)
(9)
Уравнение (9) выражает эллипс при R<n, гиперболу при
R>n и параболу при
R=n. Для
вычерчивания конических сечений по заданным параметрам a, b, p параметры настройки механизма определяются по тем же
формулам (7).
Из (6) видно, что приведенные механизмы позволяют воспроизводить участки
конических сечений со сколь угодно большими осями a, b и недоступным
центром, находящимся за пределами чертежа (при обработке – за пределами станка).
Метод проективной геометрии весьма
эффективны при проектировании направляющих механизмов; Они позволяют получать
новые оригинальные конструкции. Такие механизмы находят применение в качестве
узлов машин–автоматов, манипуляторов ПР, устройствах для обработки
криволинейных профилей и др..
Литература
Материалы патентной литературы, БергерЕ.Э.
и др. авт. св. №630096, №648452, №1100150, №1100151.