Технические науки/12. Автоматизированные системы управления на производстве.

Чумаченко С.В.

Костанайский государственный университет имени А. Байтурсынова,

Казахстан

Нахождение системы управления на колебательной

границе устойчивости

Автоматизация – одно из главных направлений научно-технического прогресса и важное средство повышения эффективности производства. Одна из важнейших характеристик систем управления - устойчивость, которая напрямую связана с работоспособностью. Неустойчивая система не выполняет функции управления и является неэффективной. Большое влияние на устойчивость оказывает обратная связь. Неустойчивость систем управления возникает из-за неправильного или очень сильного действия главной обратной связи - при выполнении ее положительной вместо отрицательной, а также при большой инерционность элементов замкнутого контура.

Для определения устойчивости используют экспериментальный и аналитический методы определения устойчивости.

При использовании экспериментального метода определения устойчивости необходимо иметь действующую систему и достаточно точную и чувствительную аппаратуру: для формирования и фиксации воздействий на систему и регистрации поведения системы после снятия воздействий. Данный метод определения устойчивости налагает следующие ограничения на технологический процесс: достаточно медленное протекание; безопасность. Данный способ определения устойчивости может применяться при переналадке и частичной модернизации оборудования.

Аналитические методы определения устойчивости используют при проектировании систем управления.

При определении устойчивости по расположению корней характеристического управления свободное движение системы описывается однородным дифференциальным уравнением:

. (1)

Вынужденная составляющая выходной величины, зависящая от вида внешнего воздействия на устойчивость системы не влияет.

Решение уравнения (1) равно сумме:

(2)

где C_k – постоянные, зависящие от начальных условий; p_k – корни характеристического уравнения .

Мнимая ось является границей устойчивости в плоскости корней. Если хотя бы один корень является «правым», то система будет неустойчивой. Если есть пара чисто мнимых корней, а все остальные корни «левые», то система находится на колебательной границе устойчивости. Если есть нулевой корень, то система находится на апериодической границе устойчивости. Если таких корней два, то система неустойчива [1]. Следовательно, системы у которых в характеристическом уравнении можно вынести за скобку р² являются неустойчивыми. Если характеристическое уравнение системы имеет порядок выше третьего, то найти его корни затруднительно, т.к. отсутствуют общие формулы нахождения корней через коэффициенты уравнений [2].

Для определения устойчивости систем управления применяют различные критерии устойчивости, которые обладают достоинствами и недостатками.

Применение алгебраического критерия Гурвица для степеней выше четвертой до недавнего времени было трудоемким, однако в настоящее время в связи с развитием вычислительной техники данное ограничение не является актуальным. Критерии Гурвица и Михайлова не позволяют определить количество «правых» корней характеристического уравнения.

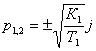Рассмотрим следующий частный случай: характеристическое уравнение системы имеет вид: . Корни данного уравнения: , , , из чего наглядно видно, что данное уравнение имеет два чисто мнимых корня, остальные два являются «левыми» и, следовательно, система находится на колебательной границе устойчивости по расположению корней характеристического уравнения.

Заполним таблицу Рауса, преобразовав данное уравнение в вид: .

Таблица Рауса будет иметь следующий вид:

			0
		0	0
		0	0
0	0	0	0
?	?	?	?

При нахождении коэффициентов 5-ой строки таблицы, при определении строчного коэффициента получаем деление на нуль ().

Отсюда можно сделать вывод: если в строке с номером n (в нашем случае n=4) появляются нули, то такая система находится на колебательной границе устойчивости [2].

Литература:

1. Сенигов П.Н. Теория автоматического управления: Конспект лекций. - Челябинск: ЮУрГУ, 2001

2. Теория автоматического управления: учеб. пособие / М.М. Савин, В.С. Елсуков, О.Н. Пятина; под. ред. д.т.н., проф. В.И. Лачина. - Ростов н/Д: Феникс, 2007