Технические науки / 12.Автоматизированные системы управления на производстве

Денисенко В.С.,  студент 4-го курсу напряму. 6.050202 

"Автоматизоване управління технологічними процесами"

Національний університет харчових технологій, м. Київ

ВИКОРИСТАННЯ МЕТОДУ ЗОЛОТОГО ПЕРЕРІЗУ ДЛЯ ВИЗНАЧЕННЯ ОПТИМАЛЬНИХ ПАРАМЕТРІВ ОБ’ЄКТІВ АВТОМАТИЗАЦІЇ

 

Не дивлячись на те, що безумовна оптимізація функції однієї змінної найбільш простий тип оптимізаційних задач, вона займає центральне місце в теорії оптимізації як з теоретичної так і з практичної точки зору. Це пов’язано з тим, що задачі одно параметричної оптимізації достатньо часто зустрічаються в інженерній практиці і, окрім того, знаходять своє застосування при реалізації більш складних інтерактивних процедур багато параметричної оптимізації.         На перший погляд здається, що задача мінімізації функції однієї змінної являється достатньо елементарною. Насправді, якщо функція (цільова), котру потрібно мінімізувати на відрізку, диференційована, то достатньо знайти нулі похідної, приєднати к ним кінці відрізку, виділити із цих точок локальні мінімуми і, нарешті, серед останніх знайти ту точку, в котрій досягається абсолютний мінімум. Однак для широкого класу функцій ця задача не така ж і проста. По-перше, задача вирішення рівняння може виявитись складною. З іншої сторони, в практичних задачах часто не відомо, чи являється диференційованою функція. В силу цього велике значення набирають методи мінімізації, які не вимагають обчислення похідної [1].   

 Метод золотого перерізу вигідно застосовувати в тих випадках коли невідома точне завдання кількості експериментів, наприклад як в методі Кіфера. Золотий перетин - співвідношення двох величин, рівне співвідношенню їх суми до більшої з даних величин.

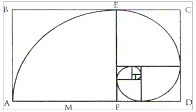
Image16.gif

Рис. 1. Представлення золотого перерізу

Золотий прямокутник утворюється при поділі відрізку АD в такій точці F, що площа прямокутника, одною стороною якого є весь відрізок, а іншою — менший з відрізків, дорівнює площі квадрата з більшим відрізком як стороною (|АD| * |FD| = |AF|2). Або ж    (Рис.1)  [2].

         Вперше метод золотого перерізу був представлений, американським математиком, Джеком Кіфером в 1953 році. Опишемо сам метод: нехай задана функція  Тоді для того щоб знайти визначене значення цієї функції на заданому відрізку, відповідаючи критерію пошуку (наприклад мінімуму), розглядуваний відрізок ділиться в пропорції золотого перерізу в обох напрямках, тобто вибираються дві точки такі, що \frac{b-a}{b-x_1}=\frac{b-a}{x_2-a}=\varphi=\frac{1+\sqrt{5}}{2}=1.618\ldots,                                                        де \varphi\! — пропорція золотого перерізу.                                                                        Таким чином:

\begin{array}{ccc} x_1 &=& b-\frac{(b-a)}{\varphi}\\ x_2 &=& a+\frac{(b-a)}{\varphi} \end{array}\!

Тобто точка x_1\! ділить відрізок [a,\;x_2]\! у відношенні золотого перерізу. Аналогічно x_2\! ділить відрізок [x_1,\;b]\! в той же пропорції. Ця властивість і використовується для побудови ітераційного процесу. Принцип вибору проміжних точок методу золотого перерізу представлений на рис. 2.

Golden_ratio.PNG

Рис. 2. Ілюстрація вибору проміжних точок на відрізку

Алгоритм методу золотого перерізу:

1.       На першій ітерації заданий відрізок ділиться двома симетричними відносно його центру точками і розраховуються значення в цих точках. 2. Після чого той з кінців відрізка, до якого серед двох знову поставлених точок ближче виявилася та, значення в якій максимально (для випадку пошуку мінімуму), відкидають. 3. На наступній ітерації в силу показаної вище властивості золотого перетину вже треба шукати всього одну нову точку. 4. Процедура продовжується до тих пір, поки не буде досягнута задана точність.

Формалізуємо метод Золотого перерізу:

·                   Крок 1. Задаються початкові границі відрізка а a,\;b\! и точність \varepsilon\!.

·                   Крок 2. Розраховують початкові точки ділення:  x_1 = b-\frac{(b-a)}{\varphi},\quad x_2 = a+\frac{(b-a)}{\varphi}\!

 і значення в них цільової функції: y_1=f(x_1),\;y_2=f(x_2)\!. Якщо y_1 \ge y_2\! (для пошуку максимуму змінити нерівність на  y_1 \le y_2\!), то a=x_1 \!. Інакше b=x_2\!.

o                  Крок 3. Якщо  |b-a|<\varepsilon \!, то  x=\frac{a+b}{2}\! і зупинимося. Інакше повертаємось до кроку 2.  [3]                                    

Можемо зробити висновок, що метод золотого перерізу доречно використовувати для визначення оптимальних параметрів об’єктів автоматизації, які представленні деякою функцією з заданим відрізком їх пошуку. Метод не дає занадто точної оптимізації шуканого параметра, але його можна використовувати для значень некритичних параметрів через його легкість та простоту.

Література:

1.     Лаврус В. Золотий переріз / В. Лаврус. – К.:Наука. – 2000. – 218 с.

2.     Аверьянов Г.П. САПР в электрофизике. Часть Ι. Основы автоматизации проектирования  / Г.П. Аверьянов, В.А. Будин, В.В. Дмитриева. – М.: МИФИ. – 2001. – 114 с.

3.     Джон Г. Мэтьюз Численные методы. Использование MATLAB / Мэтьюз Джон Г., Финк Куртис Д. – М, СПб: «Вильямс», 2001. – 716 с.