Технические науки/6. Электротехника и радиоэлектроника
Ст. преп.
Мирзакулова Ш.А.
Алматинский
университет энергетики и связи
ИССЛЕДОВАНИЕ СЕТЕВОГО ТРАФИКА
ДАННЫХ В ПАКЕТЕ AtteStat
Для исследования автокорреляции сетевого
трафика распределения межпакетных интервалов протокола ARP (Address
Resolution Protocol) применен пакет анализа данных AtteStat, которая выполнена в виде
надстройки к электронным таблицам Microsoft Excel [1].
Автокорреляция – это статистическая
взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом по
времени.
Для проверки рядов на
автокорреляцию первого порядка применим статистический критерий DW известной статистики Durbin-Watson дважды (для исходного и агрегированного ряда с параметром
агрегирования m=2).
На рисунке 1 представлен исходный ряд, а
на рисунке 2 его автокоррелограмма.
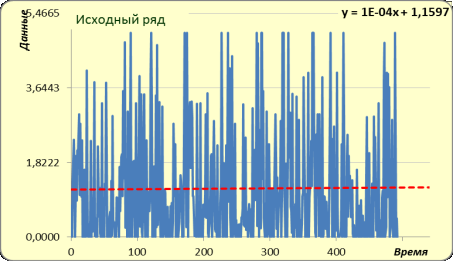
Рисунок 1 – Исходный ряд
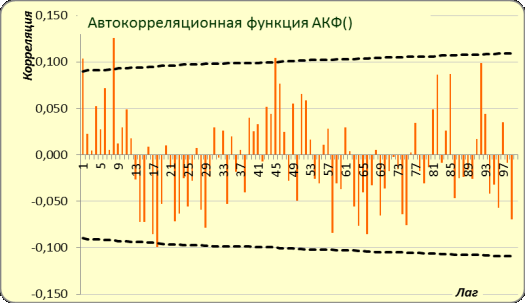
Рисунок 2 – Автокоррелограмма исходного ряда
При этом получен критерий DW равный значению 1,035 (DL=1,62; DU=1,035). Автокорреляция положительна, так как критерий
DW меньше значения DL [2].
Осуществим процесс агрегирования ряда ARP
(рисунок 3) и построим автокоррелограмму агрегированного ряда (рисунок 4).
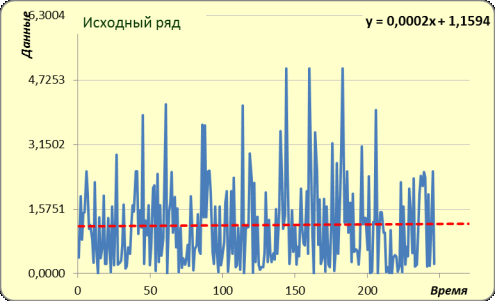
Рисунок 3 – Агрегированный ряд с параметром
агрегирования m=2
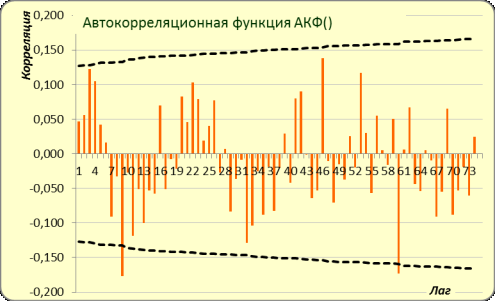
Рисунок 4 – Автокоррелограмма агрегированного ряда m=2
При этом получена оценка критерия DW=0,86 (DL=1,65; DU=1,69). Автокорреляция положительна.
Выводы: автокоррелограмма показывает
численно и графически автокорреляционную функцию (АКФ). Исследованный трафик
характеризуется инвариантностью АКФ при изменении уровня агрегирования. Ряд
имеет медленно убывающую зависимость. Это
строго самоподобный в широком смысле процесс.
Литература:
1. Гайдышев И.П. Моделирование
стохастических и детерминированных систем: Руководство пользователя программы AtteStat. – Курган, 2013. – 490 с.
2. Алехин Е.И. Основы эконометрики. Конспект
лекций. Методические рекомендации студентам факультета экономики и управления
ОГУ. ГОУ ВПО «Орловский государственный университет» Кафедра математики и
информатики, 2007. – 109 с.