Технические науки/6. Электротехника и радиоэлектроника

Ст. преп. Мирзакулова Ш.А.

Алматинский университет энергетики и связи

СТАТИСТИЧЕСКАЯ ПРОВЕРКА

ЭМПИРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ ПАКЕТОВ ПРОТОКОЛА TCP ЗАКОНУ ПУАССОНА

Осуществим проверку соответствия количества событий, измеренных на интервале на протяжении пяти часов эмпирического распределения пакетов протокола TCP (Transmission Control Protocol) распределению Пуассона в программном пакете Statistica. Объем выборки составил 158 пакетов.

На рисунке 1 представлено окно программы с вложенными данными.

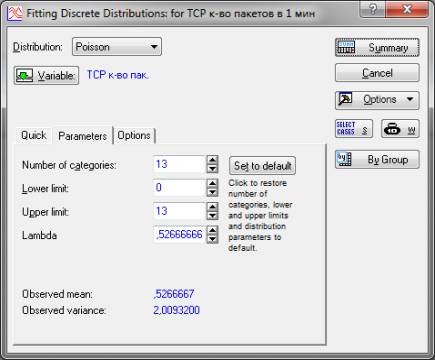
Рисунок 1 – Параметры эмпирического распределения ТСР

На рисунке 2 представлен график, на котором построена гистограмма интенсивности количества пакетов ТСР в минуту с наложенной на нее гистограммы распределения Пуассона с параметрами эмпирического распределения. В верхней части таблицы отображены значение интенсивности и оценка критерия Колмогорова-Смирнова D_эксп = 0,59057 (максимальное расстояние между эмпирической и теоритической Пуассона функциями) при экспериментально рассчитанном уровне значимости р<0,01 (очень надежного).

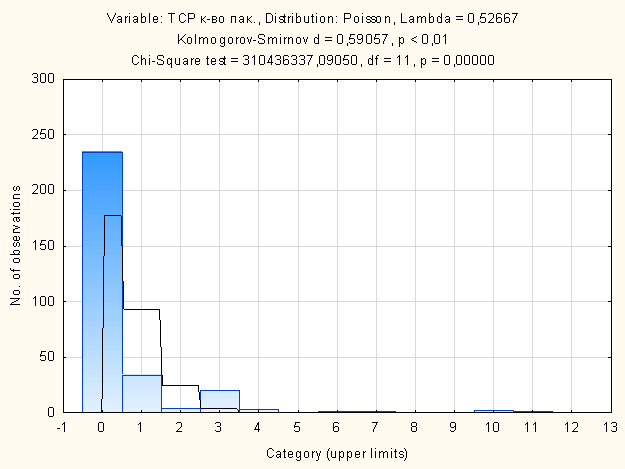
Рисунок 2 – Подгонка распределения Пуассона на распределение интенсивности пакетов ТСР

Форма гистограммы на рисунке 2 показывает, что не точно распределение интенсивности ТСР аппроксимировано распределением Пуассона, которое отмечено красным цветом.

Одно выборочный критерий Колмогорова-Смирнова в качестве меры расхождения между теоретическим и эмпирическим распределениями рассматривает максимальное значение абсолютной величины разности между эмпирической и теоретической функцией распределения.

Если D статистика Колмогорова-Смирнова значима, то гипотеза о том, что соответствующее распределение соответствует распределению Пуассона, должна быть отвергнута. В специальной таблице «Критические значения критерия Колмогорова-Смирнова при сопоставлении эмпирического распределения с теоретическим» при объеме выборки и значении р=0,01 показано, что [1]

.

Вывод: так как больше , то гипотеза о достоверных различиях принимается. Следовательно, интенсивность количества событий на этом интервале (количества пакетов ТСР) не распределены по закону Пуассона.

Литература:

1. Чубуков Ж. А., Угольник Т. С., Описательная статистика: учебно-методическое пособие для студентов всех факультетов медицинских вузов, аспирантов, магистрантов, соискателей и преподавателей. – Гомель: учреждение образования «Гомельский государственный медицинский университет», 2012. — 28 с.